Корреляция случайных величин — различия между версиями
(→Свойства корреляции) |
(→Свойства корреляции) |
||
| Строка 24: | Строка 24: | ||
|proof= | |proof= | ||
| − | Для | + | Для доказательства используем свойства ковариации |
<tex>Cov^2(\eta, \xi) \le \sigma_\eta ^2\sigma_\xi ^2</tex> | <tex>Cov^2(\eta, \xi) \le \sigma_\eta ^2\sigma_\xi ^2</tex> | ||
| − | из этого | + | из этого выходит <tex> {Cov^2(\eta,\xi)\over(\sigma_\eta ^2\sigma_\xi ^2)} \le 1</tex> |
при условии, конечно, что знаменатель не обращается в нуль. | при условии, конечно, что знаменатель не обращается в нуль. | ||
| − | <tex>Corr^2(\eta,\xi) \le 1</tex> | + | <tex>Corr^2(\eta,\xi) \le 1</tex> |
<tex>-1 \le Corr(\eta,\xi) \le 1</tex> | <tex>-1 \le Corr(\eta,\xi) \le 1</tex> | ||
Версия 20:35, 12 января 2013
Содержание
Определение
| Определение: |
Корреляция случайных величин: пусть — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их корреляция определяется следующим образом:
|
Вычисление
Заметим, что
Свойства корреляции
| Утверждение: |
Корреляция симметрична:
|
|
|
| Утверждение: |
Корреляция лежит на отрезке : |
|
Для доказательства используем свойства ковариации из этого выходит при условии, конечно, что знаменатель не обращается в нуль.
|
| Утверждение: |
Если , то и линейно зависимые |
|
Для доказательство используем доказательство свойства ковариации. Так как у нас то это обозначает что равенство на этом неравенстве выполняется только при условии что дискриминант равен нулю т.е. имеет один корень . Из этого выходят единственная случая это может произойти, если ; Ясно что и линейно зависимы. |
| Утверждение: |
Если и линейно зависимы то . |
|
Предположим что . Потом, мы имеем что ; и так . Кроме того, по свойствам дисперсии, Из этого следует, что , ясно что это равно на , знак зависит от знака . |
| Утверждение: |
Если независимые случайные величины, то
|
|
Пусть и - независимые величины. Тогда , где - их математическое ожидание. Получаем: Но обратное неверно: Пусть - случайная величина, распределенная симметрично около 0, а . , но и - зависимые величины. |
Примеры
В общем смысле корреляция - это зависимость между случайными величинами, когда изменение одной влечет изменение распределения другой.
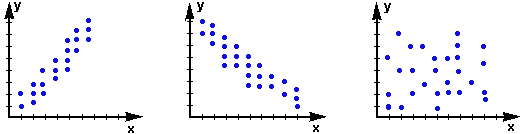
Определение корреляции по диаграмме
1. Соответственно, на первом графике изображена положительная корреляция, когда увеличение Y ведет к постепенному увеличению X.
2. Второй график отображает отрицательную корреляцию, когда увеличение X воздействует на постепенное уменьшение Y.
3. Третий график показывает, что X и Y связаны слабо, их распределение не зависит от изменения друг друга, поэтому корреляция между ними будет равна 0.
Определение корреляции по таблице
Рассмотрим 2 случайные величины: курс акций нефтедобывающей компании (X) и цены на нефть (Y).
| X | 2003,6 | 2013,2 | 2007,6 | 2007,4 | 2039,9 | 2025 | 2007 | 2017 | 2015,6 | 2011 |
|---|---|---|---|---|---|---|---|---|---|---|
| Y | 108,4 | 107,96 | 108,88 | 110,44 | 110,2 | 108,97 | 109,15 | 108,8 | 111,2 | 110,23 |
Для упрощения вычислений определим X и Y как равновероятные случайные величины. Тогда их математическое ожидание и дисперсию легко посчитать:
Используя формулу, определяем, что корреляция между величинами X и Y составляет 0,240935496, т.е. 24%.