|
|
| Строка 1: |
Строка 1: |
| − | TODO:
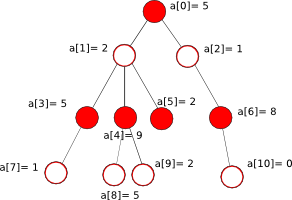
| + | Рассмотрим динамику по дереву на примере задачи о максимальном независимом множестве в дереве. |
| − | * Merge со статьей berkeley
| + | [[Файл:Independent_set_tree.png|100px|right|frame|Независимый набор из красных вершин]] |
| − | * Добавить еще примеры
| + | {{Определение |
| − | * Конспект с лекции. Добавить затронутые темы.
| + | |neat = 1 - параметр нужен для того, чтобы определение не растягивалось на всю страницу(не обязательно) |
| − | | + | |definition=Пусть дано подвешенное за корень дерево, имеющее веса на каждой из ее вершин. Необходимо выбрать такое множество вершин, что бы сумма значений была максимальной и при этом выбранные вершины не являлись бы друг-другу соседями (отец-сын). |
| − | Дерево {{---}} очередная структура данных, на которой можно увидеть принцип разбиения решения на подзадачи. Представьте дерево <tex>T</tex> с <tex>n</tex> вершинами. Так как в поддеревья <tex>T</tex> входят все потомки корня, то поддеревьев в <tex>T</tex> ровно столько же, сколько и вершин (<tex>n</tex> в данном случае).
| + | }} |
| − | == Максимальное независимое множество в дереве ==
| |
| − | | |
| − | Если данный граф является деревом, то задача о независимом множестве эффективно решается методом [[динамическое программирование|динамического программирования]].
| |
| − | | |
| − | === Оптимальная подструктура задачи ===
| |
| − | | |
| − | Структура дерева сама подсказывает решение задачи: Обозначим корнем дерева любую вершину и назовем её <tex>r</tex>. Пусть <tex>I(u)</tex> обозначает размер максимального независимого множества вершин поддерева, корнем которого является вершина <tex>u</tex>. Тогда ответом на задачу будет являться <tex>I(r)</tex>.
| |
| − | | |
| − | Нетрудно видеть, что если мы включаем вершину ''u'' в максимальное независимое множество, то его [[Мощность множества|мощность]] увеличивается на 1, но его детей мы брать не можем (так как они соединены ребром с вершиной ''u''); если же мы не включаем эту вершину, то мощность максимального независимого множества будет равна сумме размеров независимых множеств детей этой вершины. Остается только выбрать максимум из этих двух вариантов, чтобы получить решение задачи:
| |
| − | : <tex>I(u) = \max\left\{1\ +\ \sum_{\text{grandchild}\ w\ of\ u}I(w),\ \sum_{\text{child}\ w\ of\ u}I(w) \right\},</tex>
| |
| − | где grandchild обозначает всякого «внука» вершины, а child обозначает всякого потомка вершины.
| |
| − | | |
| − | === Псевдокод ===
| |
| − | Считаем, что в вершине u хранится <tex>I(u)</tex>:
| |
| − | | |
| − | get_independent_set(Node u)
| |
| − | если I(u) уже посчитано, то возвратить I(u)
| |
| − | //мощность множества, которое можно получить, если не брать вершину u
| |
| − | children_sum = 0
| |
| − | //мощность множества, которое можно получить, если взять вершину u
| |
| − | grandchildren_sum = 0
| |
| − | //цикл по всем детям
| |
| − | for i := 1 to child_num do
| |
| − | children_sum = children_sum + get_independent_set(children[i])
| |
| − | //цикл по всем внукам
| |
| − | for i:= 1 to grandchildren_num
| |
| − | grandchildren_sum = grandchildren_sum + get_independent_set(grandchildren[i])
| |
| − | //запоминаем, чтобы не персчитывать ещё раз
| |
| − | I(u) = max(1 + grandchildren_sum, children_sum)
| |
| − | возвратить I(u)
| |
| − | | |
| − | Вызов get_independent_set(''r'') даст ответ на задачу. Время выполнения алгоритма, очевидно, <tex>O(|V| + |E|)</tex>.
| |