Эквивалентность состояний ДКА

Определение:

Два автомата [math] \mathcal{A}_1 = \langle Q_1,\Sigma,\delta_1,s_{1}, T_1\subseteq Q_1 \rangle [/math] и [math]\mathcal{A}_2 = \langle Q_2,\Sigma,\delta_2,s_{2}, T_2\subseteq Q_2 \rangle [/math] называются эквивалентными, если они распознают один и тот же язык над алфавитом [math]\Sigma[/math], то есть [math]\mathcal{L}(\mathcal{A}_1) = \mathcal{L}(\mathcal{A}_2)[/math].

Определение:

Слово [math]z \in \Sigma^*[/math] различает два состояния [math]q_i[/math] и [math]q_j[/math], если [math] \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow (t_1 \notin T \Leftrightarrow t_2 \in T) [/math].

Определение:

Два состояния [math]q_i[/math] и [math]q_j[/math] называются эквивалентными [math](q_i \sim q_j)[/math], если не существует строки, которая их различает, то есть [math]\forall z \in \Sigma^*[/math] верно, что [math] \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow (t_1 \in T \Leftrightarrow t_2 \in T) [/math].

Заметим, что эквивалентность состояний действительно является отношением эквивалентности. Так как [math] \Leftrightarrow [/math] (равносильность) является отношением эквивалентности и в детерминированном автомате всегда существует путь по любому слову, описанное нами отношение является отношением эквивалентности.

Лемма:

[math] \mathcal{A} = \langle Q, \Sigma, \delta, s, T \rangle [/math], [math] p_1, p_2, q_1, q_2 \in Q [/math], [math] q_i = \delta(p_i, c) [/math], [math] w \in \Sigma^*[/math] различает [math] q_1 [/math] и [math] q_2 [/math]. Тогда [math]cw[/math] различает [math] p_1 [/math] и [math] p_2 [/math].

Доказательство:

[math]\triangleright[/math]

[math] \langle p_i, cw \rangle \vdash \langle q_i, w \rangle \vdash^* \langle t_i, \varepsilon \rangle [/math] А значит, по условию различимости для [math] q_1 [/math] и [math] q_2[/math] , [math] t_1 \in T \Leftrightarrow t_2 \notin T [/math]

[math]\triangleleft[/math]

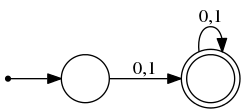
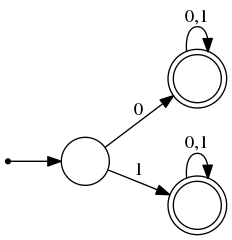
Пример

Эти два автомата принимают слова из языка слов длины не меньше одного, состоящих из символов алфавита [math] \lbrace 0, 1\rbrace [/math]. Стартовые и все допускающие состояния автоматов эквивалентны между собой.

Проверка ДКА на эквивалентность

Заданы два автомата: [math] \mathcal{A}_1 [/math] со стартовым состоянием [math] s_1 [/math] и [math] \mathcal{A}_2 [/math] со стартовым состоянием [math] s_2 [/math] соответственно. Нужно проверить их на эквивалентность. Для этого построим автомат [math] \mathcal{A} [/math], содержащий все состояния обоих автоматов и изначальные переходы между ними:

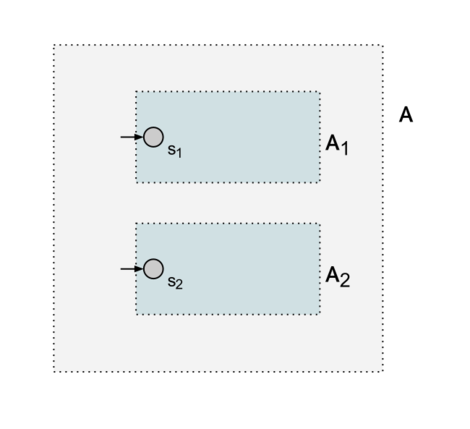
Осталось лишь проверить в полученном автомате состояния [math] s_1 [/math] и [math] s_2 [/math] на эквивалентность. Их эквивалентность совпадает с эквивалентностью автоматов [math] \mathcal{A}_1 [/math] и [math] \mathcal{A}_2 [/math].