Минимизация ДНФ с помощью покрытий гиперкуба и карт Карно — различия между версиями
(Новая страница: «Известны два способа минимизации дизъюнктивных нормальных форм: == Визуализация гиперкуб…») |
|||
| Строка 15: | Строка 15: | ||
В итоге нашу изначальную ДНФ можно записать как <math>(Y) \or (X \and \neg Y \and Z)</math>. | В итоге нашу изначальную ДНФ можно записать как <math>(Y) \or (X \and \neg Y \and Z)</math>. | ||
| + | |||
| + | == Карты Карно == | ||
| + | |||
| + | Этот способ работает при количестве переменных не более 4. | ||
| + | |||
| + | Мы рисуем следующую таблицу n*n, где n — количество переменных: | ||
| + | {| border="1" | ||
| + | | | ||
| + | | | ||
| + | !w | ||
| + | !w | ||
| + | !не w | ||
| + | !не w | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | !z | ||
| + | !не z | ||
| + | !не z | ||
| + | !z | ||
| + | |- | ||
| + | !y | ||
| + | !x | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | !y | ||
| + | !не x | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | !не y | ||
| + | !не x | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | !не y | ||
| + | !x | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |} | ||
| + | Теперь для каждого конъюнкта мы помечаем соответствующую ему ячейку таблицы. Например, ДНФ | ||
| + | <br> | ||
| + | <br> | ||
| + | <math>(X \and Y \and Z \and W) \or (X \and Y \and \neg Z \and W) \or (X \and Y \and \neg Z \and \neg W) \or (X \and Y \and Z \and \neg W) \or (\neg X \and Y \and Z \and W) \or (\neg X \and Y \and \neg Z \and W) \or (\neg X \and Y \and \neg Z \and \neg W) \or (\neg X \and Y \and Z \and \neg W) \or (X \and \neg Y \and Z \and W) \or (X \and \neg Y \and \neg Z \and W) \or (\neg X \and \neg Y \and \neg Z \and \neg W)</math> | ||
| + | <br> | ||
| + | <br> | ||
| + | будет выглядеть на картах Карно так: | ||
| + | <br> | ||
| + | <br> | ||
| + | {| border="1" | ||
| + | | | ||
| + | | | ||
| + | !w | ||
| + | !w | ||
| + | !не w | ||
| + | !не w | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | !z | ||
| + | !не z | ||
| + | !не z | ||
| + | !z | ||
| + | |- | ||
| + | !y | ||
| + | !x | ||
| + | |1 | ||
| + | |1 | ||
| + | |1 | ||
| + | |1 | ||
| + | |- | ||
| + | !y | ||
| + | !не x | ||
| + | |1 | ||
| + | |1 | ||
| + | |1 | ||
| + | |1 | ||
| + | |- | ||
| + | !не y | ||
| + | !не x | ||
| + | | | ||
| + | | | ||
| + | |1 | ||
| + | | | ||
| + | |- | ||
| + | !не y | ||
| + | !x | ||
| + | |1 | ||
| + | |1 | ||
| + | | | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
| + | *Теперь мы покрываем непересекающиеся прямоугольниками с максимальной площадью те ячейки карт Карно, которые содержат в себе единицу до тех пор, пока не покроем все такие ячейки (для карт Карно на примере это выглядело бы так:) | ||
| + | <br> | ||
| + | {| border="1" | ||
| + | | | ||
| + | | | ||
| + | !w | ||
| + | !w | ||
| + | !не w | ||
| + | !не w | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | !z | ||
| + | !не z | ||
| + | !не z | ||
| + | !z | ||
| + | |- | ||
| + | !y | ||
| + | !x | ||
| + | |style="background:#F4A460"|1 | ||
| + | |style="background:#F4A460"|1 | ||
| + | |style="background:#F4A460"|1 | ||
| + | |style="background:#F4A460"|1 | ||
| + | |- | ||
| + | !y | ||
| + | !не x | ||
| + | |style="background:#F4A460"|1 | ||
| + | |style="background:#F4A460"|1 | ||
| + | |style="background:#F4A460"|1 | ||
| + | |style="background:#F4A460"|1 | ||
| + | |- | ||
| + | !не y | ||
| + | !не x | ||
| + | | | ||
| + | | | ||
| + | |style="background:#7FFFD4"|1 | ||
| + | | | ||
| + | |- | ||
| + | !не y | ||
| + | !x | ||
| + | |style="background:#D2B48C"|1 | ||
| + | |style="background:#D2B48C"|1 | ||
| + | | | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
| + | *После этого записываем каждый | ||
Версия 05:43, 3 октября 2010
Известны два способа минимизации дизъюнктивных нормальных форм:
Визуализация гиперкубами
Этот способ работает при количестве переменных не больше трёх (в противном случае нам придётся вводить четвёртое и следующие за ним измерения для представления фигур). Сначала мы рисуем куб в системе отсчёта Oxyz (названия координатных осей должны соответствовать названиям переменных). Затем каждую вершину обрабатываем следующим образом:
- Если у нас конъюнкт, переменные в котором равны соответствующим координатам вершины (пример: вершине с координатами (0,1,1) соответствует конъюнкт , он равен единице при X=0, Y=1 и Z=1), то в эту вершину мы помещаем закрашенный чёрным кружок.
- В противном случае мы помещаем в вершину закрашенный белый кружок.
Например, для такой ДНФ: мы получим такой гиперкуб: 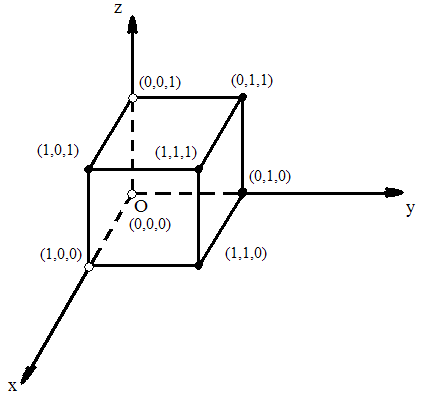
Далее обработка гиперкуба идёт следующим образом:
- Если в данном гиперкубе есть грань, все вершины на которой закрашены чёрным, то мы можем записать её в качестве конъюнкта, где будет только переменная с неизменяющейся соответствующей ей координатой, например, грань, на которой лежат закрашенные вершины (0,1,1), (0,1,0), (1,1,0) и (1,1,1) мы можем записать как конъюнкт .
- Если в данном гиперкубе есть ребро, все вершины на котором закрашены чёрным, то мы можем записать его в качестве конъюнкта, где будут только переменные с неизменяющимися соответствующим им координатами, например, ребро, соединяющее закрашенные вершины (0,1,1) и (1,1,1) мы можем записать как конъюнкт .
В итоге нашу изначальную ДНФ можно записать как .
Карты Карно
Этот способ работает при количестве переменных не более 4.
Мы рисуем следующую таблицу n*n, где n — количество переменных:
| w | w | не w | не w | ||
|---|---|---|---|---|---|
| z | не z | не z | z | ||
| y | x | ||||
| y | не x | ||||
| не y | не x | ||||
| не y | x |
Теперь для каждого конъюнкта мы помечаем соответствующую ему ячейку таблицы. Например, ДНФ
будет выглядеть на картах Карно так:
| w | w | не w | не w | ||
|---|---|---|---|---|---|
| z | не z | не z | z | ||
| y | x | 1 | 1 | 1 | 1 |
| y | не x | 1 | 1 | 1 | 1 |
| не y | не x | 1 | |||
| не y | x | 1 | 1 |
- Теперь мы покрываем непересекающиеся прямоугольниками с максимальной площадью те ячейки карт Карно, которые содержат в себе единицу до тех пор, пока не покроем все такие ячейки (для карт Карно на примере это выглядело бы так:)
| w | w | не w | не w | ||
|---|---|---|---|---|---|
| z | не z | не z | z | ||
| y | x | 1 | 1 | 1 | 1 |
| y | не x | 1 | 1 | 1 | 1 |
| не y | не x | 1 | |||
| не y | x | 1 | 1 |
- После этого записываем каждый