1precripi1Lmax — различия между версиями
| Строка 16: | Строка 16: | ||
==Доказательство== | ==Доказательство== | ||
| + | [[Файл:1precripi1Lmax.png|500px|thumb|right|Пояснение]] | ||
Пусть существует оптимальное расписание <tex> S^* </tex>. В этом расписании работа выполняется тогда, когда она появилась, либо когда закончилась другая работа. | Пусть существует оптимальное расписание <tex> S^* </tex>. В этом расписании работа выполняется тогда, когда она появилась, либо когда закончилась другая работа. | ||
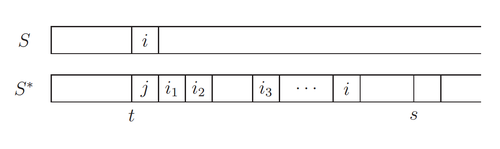
Рассмотрим такое расписание <tex>S^*</tex>, которое как можно дольше совпадает с расписанием S, построенным алгоритмом. Пусть <tex> t~-</tex> первый момент времени, когда в расписании <tex>S</tex> начинает выполняться работа <tex>i</tex>, а в расписании <tex>S^*</tex> работа <tex>j</tex> (причем <tex> i \ne j </tex>). Мы знаем, что <tex> r_i, r_j \le t </tex>, а значит <tex> d_i \le d_j </tex> (поскольку при построении мы выбираем минимальное доступное <tex> d_k </tex>). Пусть <tex> i_1, i_2, ..., i_l~-</tex> все работы, которые находятся в расписании <tex>S^*</tex> между работами <tex>j</tex> и <tex>i</tex> и являются наследниками работы <tex>j</tex>. Кроме того, предположим, что эти работы упорядочены по времени начала выполнения. Теперь, если мы поставим работу <tex>i_l</tex> вместо <tex>i, i_{l-1}</tex> вместо <tex>i_{l}, ..., j</tex> вместо <tex>i_1, i</tex> вместо <tex>j</tex>, то мы снова получим возможное оптимальное расписание <tex> S' </tex>. так как <tex> d_i \le d_j \le d_v </tex>, где <tex> v \in {i_1, i_2, ... i_l} </tex>. Последнее неравенство имеет место быть, поскольку все работы <tex>i_v</tex> являются наследниками работы <tex>j</tex>. | Рассмотрим такое расписание <tex>S^*</tex>, которое как можно дольше совпадает с расписанием S, построенным алгоритмом. Пусть <tex> t~-</tex> первый момент времени, когда в расписании <tex>S</tex> начинает выполняться работа <tex>i</tex>, а в расписании <tex>S^*</tex> работа <tex>j</tex> (причем <tex> i \ne j </tex>). Мы знаем, что <tex> r_i, r_j \le t </tex>, а значит <tex> d_i \le d_j </tex> (поскольку при построении мы выбираем минимальное доступное <tex> d_k </tex>). Пусть <tex> i_1, i_2, ..., i_l~-</tex> все работы, которые находятся в расписании <tex>S^*</tex> между работами <tex>j</tex> и <tex>i</tex> и являются наследниками работы <tex>j</tex>. Кроме того, предположим, что эти работы упорядочены по времени начала выполнения. Теперь, если мы поставим работу <tex>i_l</tex> вместо <tex>i, i_{l-1}</tex> вместо <tex>i_{l}, ..., j</tex> вместо <tex>i_1, i</tex> вместо <tex>j</tex>, то мы снова получим возможное оптимальное расписание <tex> S' </tex>. так как <tex> d_i \le d_j \le d_v </tex>, где <tex> v \in {i_1, i_2, ... i_l} </tex>. Последнее неравенство имеет место быть, поскольку все работы <tex>i_v</tex> являются наследниками работы <tex>j</tex>. | ||
Версия 16:35, 19 июня 2013
Постановка задачи
Рассмотрим задачу:
- Дано работ и один станок.
- Для каждой работы известно её время появления . Время выполнения всех работ равно . Работа может начаться только после выполнения некоторых других работ, эта зависимость дана в виде ациклического графа.
Необходимо составить такое расписание, чтобы значение было минимальным.
Описание алгоритма
Пусть — текущий момент времени.
Для каждого очередного значения , которое изменяется от до времени окончания последней работы, будем:
- Выполнять работу из множества невыполненных работ, у которой минимально.
- Увеличиваем на один.
Доказательство
Пусть существует оптимальное расписание . В этом расписании работа выполняется тогда, когда она появилась, либо когда закончилась другая работа. Рассмотрим такое расписание , которое как можно дольше совпадает с расписанием S, построенным алгоритмом. Пусть первый момент времени, когда в расписании начинает выполняться работа , а в расписании работа (причем ). Мы знаем, что , а значит (поскольку при построении мы выбираем минимальное доступное ). Пусть все работы, которые находятся в расписании между работами и и являются наследниками работы . Кроме того, предположим, что эти работы упорядочены по времени начала выполнения. Теперь, если мы поставим работу вместо вместо вместо вместо , то мы снова получим возможное оптимальное расписание . так как , где . Последнее неравенство имеет место быть, поскольку все работы являются наследниками работы .