J2ni2Cmax — различия между версиями
Watson (обсуждение | вклад) (→Описание алгоритма) |
Watson (обсуждение | вклад) (→Описание алгоритма) |
||
| Строка 23: | Строка 23: | ||
Тогда оптимальное расписание для нашей задачи будет следующим: | Тогда оптимальное расписание для нашей задачи будет следующим: | ||
| − | + | ||
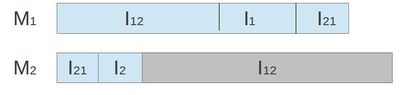
| − | <li>Расписание <tex> | + | <li>Расписание <tex>M_{2}</tex> : сначала <tex>I_{12}</tex> в соответсвии с расписанием <tex>S_{12}</tex>. Затем <tex>I_{1}</tex> в произвольном порядке. Затем <tex>I_{21}</tex> в соответсвии с <tex>S_{21}</tex>. </li> |
<li>Расписание <tex>M_{2}</tex> : сначала <tex>I_{21}</tex> в соответсвии с расписанием <tex>S_{21}</tex>. Затем <tex>I_{2}</tex> в произвольном порядке. Затем <tex>I_{12}</tex> в соответсвии с <tex>S_{12}</tex>. </li> | <li>Расписание <tex>M_{2}</tex> : сначала <tex>I_{21}</tex> в соответсвии с расписанием <tex>S_{21}</tex>. Затем <tex>I_{2}</tex> в произвольном порядке. Затем <tex>I_{12}</tex> в соответсвии с <tex>S_{12}</tex>. </li> | ||
| − | + | ||
Примечание: во время выполнения <tex>I_{21}</tex> на <tex>M_{1}</tex> или <tex>I_{12}</tex> на <tex>M_{2}</tex> могут возникнуть простои | Примечание: во время выполнения <tex>I_{21}</tex> на <tex>M_{1}</tex> или <tex>I_{12}</tex> на <tex>M_{2}</tex> могут возникнуть простои | ||
из-за того, что работа ещё не выполнилась на предыдущем станке. | из-за того, что работа ещё не выполнилась на предыдущем станке. | ||
Версия 18:57, 22 июня 2013
Содержание
Постановка задачи
Рассмотрим задачу:
- Дано работ и станка.
- Для каждой работы известно её время выполнения на каждом станке .
- Для каждой работы известна последовательность станков - порядок, в котором нужно выполнить работу.
- Для любой работы (Длина последовательности ) .
Требуется минимизировать время окончания выполнения всех работ.
Описание алгоритма
- первый станок. - второй станок.
Разобьем все работы на четыре множества:
- - множество всех работ, которые должны выполниться только на .
- - множество всех работ, которые должны выполниться только на .
- - множество всех работ, которые должны выполниться сначала на затем на .
- - множество всех работ, которые должны выполниться сначала на затем на .
Решим задачу для и для . Получим расписание и .
Тогда оптимальное расписание для нашей задачи будет следующим:
Примечание: во время выполнения на или на могут возникнуть простои из-за того, что работа ещё не выполнилась на предыдущем станке.
Доказательство корректности алгоритма
- время выполнения множества работ на станке .
- множество всех работ, которые нужно сделать хотя бы раз на -м станке. (Формально )
| Лемма: |
Расписание, построенное данным алгоритмом, обладает следующим свойством : один из станков работает без простоев. |
| Доказательство: |
|
Рассмотрим 2 варианта:
|
| Теорема: |
Расписание, построенное данным алгоритмом, является корректным и оптимальным. |
| Доказательство: |
|
Корректность алгоритма очевидна. Докажем оптимальность. Пусть, для опеределенности работает без прерываний. Рассмотрим станок на котором достигается . |
Сложность алгоритма
Время работы алгоритма равно времени работы алгоритма .
Сложность алгоритма .