Алгоритм Балабана — различия между версиями
(→Основные понятия: + Picture size) |
(add some algo) |
||
| Строка 60: | Строка 60: | ||
==Алгоритм== | ==Алгоритм== | ||
| + | |||
| + | Введем несколько дополнительных функций, чтобы упростить основной алгоритм: | ||
| + | |||
| + | ===Split=== | ||
| + | |||
| + | Пусть <tex>L = (s_1 ,..., s_k)</tex>, где <tex>s_i <_b s_{i+1}</tex> | ||
| + | <tex>Split_{a,b}(L, Q, L')</tex> | ||
| + | <tex>\{</tex> | ||
| + | <tex>L' \leftarrow 0; Q \leftarrow 0</tex> | ||
| + | '''For''' <tex>j = 1,...,k</tex> '''do''' | ||
| + | '''if''' отрезок <tex>S_j</tex> не пересекает | ||
| + | последний отрезок из <tex>Q</tex> внутри полосы <tex>\langle a, b \rangle</tex> | ||
| + | и при этом содержит её '''then''' | ||
| + | добавить <tex>s_j</tex> в конец <tex>Q;</tex> | ||
| + | '''else''' | ||
| + | добавить <tex>s_j</tex> в конец <tex>L’;</tex> | ||
| + | <tex>\}</tex> | ||
| + | |||
| + | ===Search In Strip=== | ||
==Примечания== | ==Примечания== | ||
Версия 16:36, 1 октября 2013
Алгоритм Балабана — детерминированный алгоритм, позволяющий по множеству отрезков на плоскости получить множество точек, в которых эти отрезки пересекаются.
Содержание
Введение
Решение задачи по поиску множества пересечений отрезков является одной из главных задач вычислительной геометрии. Тривиальный детерминированный алгоритм имеет временную сложность , и его суть заключается в проверке попарного пересечения отрезков. Сложнее, но эффективнее алгоритм Бентли-Оттмана [1] с оценкой сложности , в основе которого лежит метод заметающей прямой. Алгоритм, предложенный Чазелле и Едельсбруннером [2], имеет лучшую оценку , но в отличие от предыдущих методов требует квадратичной памяти. Оптимальный детерминированный алгоритм был предложен Балабаном [3] с временной оценкой сложности и памяти, где К - число пересекающихся отрезков. При количестве отрезков равным 2000 и большому количеству пересечений целесообразно использовать алгоритм Балабана. Однако в результате громоздкости и высокой сложности реализации алгоритма в большинстве практических задач используется алгоритм заметающей прямой Бентли-Оттмана.
Основные понятия
Введем некоторые обозначения. Пусть - множество всех точек пересечения отрезков из множества , а - количество таких пересечений ;
Через обозначим вертикальную полосу, которая ограничена прямыми и , а через отрезок с концами абсцисс и .
Рассмотрим взаимное расположение вертикальной полосы и отрезка .
| Определение: |
| Будем говорить, что отрезок , с концами абсцисс и :
- содержит(span) полосу , если ; |
| Определение: |
| Два отрезка и называются пересекающимися внутри полосы , если их точка пересечения лежит в пределах этой полосы. Для двух множеств отрезков и определим множество как . |
Обозначения и будут использоваться для описания подмножеств и , состоящих из пересекающихся пар отрезков в пределах полосы . Далее скобки используются для определения неупорядоченных наборов, а скобки используются для определения упорядоченных множеств.
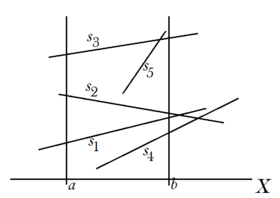
Введем отношение порядка на множестве отрезков если оба отрезка пересекают вертикальную линию и точка пересечения этой прямой с отрезком лежит ниже точки пересечения с .
− любой отрезок из содержит полосу ;
− нет пересечений отрезков внутри лестницы;
− упорядочена по отношению .
| Определение: |
| Если точка отрезка лежит между ступеньками и , тогда число называется местоположением на лестнице и обозначается как |
| Утверждение: |
Имея лестницу и множество отрезков , множество можно найти за время . Однако, если упорядочено отношением , где , тогда можно найти за время . |
Алгоритм
Введем несколько дополнительных функций, чтобы упростить основной алгоритм:
Split
Пусть , где For do if отрезок не пересекает последний отрезок из внутри полосы и при этом содержит её then добавить в конец else добавить в конец
Search In Strip
Примечания
Литература
Т.Вознюк, В.Терещенко — К построению эффективного решения задачи пересечения отрезков
Ф.Препарата, М.Шеймос — Вычислительная геометрия