Теорема Клини (совпадение классов автоматных и регулярных языков) — различия между версиями
Gromak (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
{{Теорема | {{Теорема | ||
|author=Клини | |author=Клини | ||
| − | |statement=Классы автоматных и регулярных языков совпадают. | + | |statement=Классы [[Детерминированные_конечные_автоматы#Автоматные_языки | автоматных]] и [[Регулярные языки:_два определения_и_их_эквивалентность | регулярных]] языков совпадают. |
|proof= | |proof= | ||
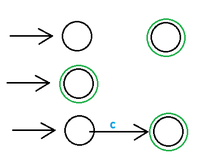
[[Файл:Reg0.png|200px|thumb|right|Автоматы для регулярных языков нулевого поколения]] | [[Файл:Reg0.png|200px|thumb|right|Автоматы для регулярных языков нулевого поколения]] | ||
| Строка 7: | Строка 7: | ||
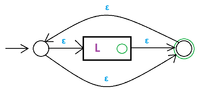
[[Файл:concat.png|200px|thumb|right|Автомат для конкатенации двух регулярных языков]] | [[Файл:concat.png|200px|thumb|right|Автомат для конкатенации двух регулярных языков]] | ||
[[Файл:Klenee.png|200px|thumb|right|Автомат для замыкания Клини регулярного языка]] | [[Файл:Klenee.png|200px|thumb|right|Автомат для замыкания Клини регулярного языка]] | ||
| − | 1. <tex> | + | 1. <tex>\mathrm{REG} \subseteq \mathrm{AUT}</tex>. |
Для доказательства будем строить автоматы, допускающие регулярные языки (см. картинки справа). При этом будем использовать индукцию по номеру поколения регулярного языка. | Для доказательства будем строить автоматы, допускающие регулярные языки (см. картинки справа). При этом будем использовать индукцию по номеру поколения регулярного языка. | ||
| Строка 18: | Строка 18: | ||
'''Индукционный переход'''. Умеем строить автоматы для языков <tex>n</tex>-ого поколения. Будем строить для <tex>n + 1</tex>. | '''Индукционный переход'''. Умеем строить автоматы для языков <tex>n</tex>-ого поколения. Будем строить для <tex>n + 1</tex>. | ||
| − | Для этого достаточно научиться строить автоматы для следующих языков (<tex>L, M \in | + | Для этого достаточно научиться строить автоматы для следующих языков (<tex>L, M \in \mathrm{R_n}</tex>): |
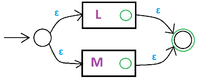
*<tex>L^\prime = L \cup M</tex>, | *<tex>L^\prime = L \cup M</tex>, | ||
*<tex>L^\prime = LM</tex>, | *<tex>L^\prime = LM</tex>, | ||
| Строка 26: | Строка 26: | ||
Итого, мы можем по регулярному выражению построить автомат, допускающий тот же язык. | Итого, мы можем по регулярному выражению построить автомат, допускающий тот же язык. | ||
| − | 2. <tex> | + | 2. <tex>\mathrm{AUT} \subseteq \mathrm{REG}</tex>. |
Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат <tex>A</tex> с набором состояний <tex>Q = \left\{1, 2, \dots n \right\}</tex>. | Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат <tex>A</tex> с набором состояний <tex>Q = \left\{1, 2, \dots n \right\}</tex>. | ||
Версия 20:26, 21 октября 2013
| Теорема (Клини): |
Классы автоматных и регулярных языков совпадают. |
| Доказательство: |
|
1. . Для доказательства будем строить автоматы, допускающие регулярные языки (см. картинки справа). При этом будем использовать индукцию по номеру поколения регулярного языка. База. . Для этого достаточно построить автоматы для трех языков:
Индукционный переход. Умеем строить автоматы для языков -ого поколения. Будем строить для . Для этого достаточно научиться строить автоматы для следующих языков ():
Заметим, что по предположению индукции автоматы для могут быть построены. Итого, мы можем по регулярному выражению построить автомат, допускающий тот же язык. 2. . Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат с набором состояний . Определим регулярные выражения, задающие следующие множества слов: , причем в качестве промежуточных вершин выступают только такие, у которых номер не более . Построим эти регулярные выражения:
Теперь нетрудно задать регулярное выражение для всего языка: , где — стартовое состояние, а — терминальные состояния исходного автомата. Таким образом, мы построили по автомату регулярное выражение, допускающее тот же самый язык. |