Алгоритм Балабана

Эта статья находится в разработке!

Алгоритм Балабана — детерминированный алгоритм, позволяющий по множеству отрезков на плоскости получить множество точек, в которых эти отрезки пересекаются.

Введение

Решение задачи по поиску множества пересечений отрезков является одной из главных задач вычислительной геометрии. Тривиальный детерминированный алгоритм имеет временную сложность [math]O(n^2)[/math], и его суть заключается в проверке попарного пересечения отрезков. Сложнее, но эффективнее алгоритм Бентли-Оттмана с оценкой сложности [math]O((n + k)\ log(n)+k)[/math], в основе которого лежит метод заметающей прямой. Алгоритм, предложенный Чазелле и Едельсбруннером , имеет лучшую оценку [math]O(n\ log(n) + k)[/math], но в отличие от предыдущих методов требует квадратичной памяти. Оптимальный детерминированный алгоритм был предложен Балабаном с временной оценкой сложности [math]O(n\ log(n) + k)[/math] и [math]O(n)[/math] памяти, где К - число пересекающихся отрезков. При количестве отрезков равным 2000 и большому количеству пересечений целесообразно использовать алгоритм Балабана. Однако в результате громоздкости и высокой сложности реализации алгоритма в большинстве практических задач используется алгоритм заметающей прямой Бентли-Оттмана.

Основные понятия

Введем некоторые обозначения. Пусть [math]Int(S)[/math] - множество всех точек пересечения отрезков из множества [math]S[/math], а [math]K = |Int(S)|[/math] - количество таких пересечений ;
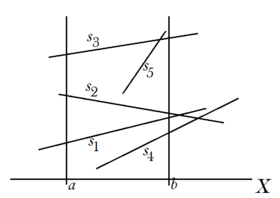
Через [math]\langle a, b \rangle[/math] обозначим вертикальную полосу, которая ограничена прямыми [math]x = a[/math] и [math]x = b[/math], а через [math]s[/math] — отрезок с вершинами в точках с абсциссами [math]l[/math] и [math]r[/math].
Рассмотрим взаимное расположение вертикальной полосы [math]\langle a, b \rangle[/math] и отрезка [math]s[/math].

Определение:

Будем говорить, что отрезок [math]s[/math], с вершинами в точках с абсциссами [math]l[/math] и [math]r[/math] : - содержит(span) полосу [math]\langle a, b \rangle[/math], если [math]l \le a \le b \le r[/math]; - внутренний(inner) для полосы [math]\langle a, b \rangle[/math], если [math]a \lt l \lt r \lt b[/math]; - пересекает(cross) полосу [math]\langle a, b \rangle[/math] в других случаях.

Определение:

Два отрезка [math]s_1[/math] и [math]s_2[/math] называются пересекающимися внутри полосы [math]\langle a, b \rangle[/math], если их точка пересечения лежит в пределах этой полосы. Для двух множеств отрезков [math]S[/math] и [math]S'[/math] определим множество [math]Int(S, S')[/math] как [math]\{ {s, s'} | (s \in S, s' \in S') \& (s \ intersect \ s') \}[/math].

[math]D = ((s_1, s_2, s_3), \langle a, b \rangle)[/math], [math]Loc(D, s_4) = 0[/math], [math]Loc(D, s_5) = 2[/math] или [math]3[/math], [math]Int(D, \{s_4,\ s_5\}) = \{\{s_3,\ s_5\}\}[/math]

Обозначения [math]Int_{a, b}(S)[/math] и [math]Int_{a, b}(S, S')[/math] будут использоваться для описания подмножеств [math]Int(S)[/math] и [math]Int(S, S')[/math], состоящих из пересекающихся пар отрезков в пределах полосы [math]\langle a, b \rangle[/math]. Далее скобки [math]\{\}[/math] используются для определения неупорядоченных наборов, а скобки [math]()[/math] используются для определения упорядоченных множеств.

Введем отношение порядка на множестве отрезков [math]s_1 \lt _b s_2[/math] если оба отрезка пересекают вертикальную линию [math]x = a[/math] и точка пересечения этой прямой с отрезком [math]s_1[/math] лежит ниже точки пересечения с [math]s_2[/math].

Определение:

Лестница [math]D[/math] — это пара [math](Q, \langle a, b \rangle)[/math], в которой отрезки из множества [math]Q[/math] удовлетворяют следующим условиям :

− любой отрезок из [math]Q[/math] содержит полосу [math]\langle a, b \rangle[/math];
− нет пересечений отрезков внутри лестницы;
− [math]Q[/math] упорядочена по отношению [math]\lt _a[/math].

Часть отрезков лестницы внутри полосы будем называть ступеньками.

Определение:

Будем называть лестницу [math]D[/math] полностью соотносимой множеству отрезков [math]S[/math], если каждый отрезок из [math]S[/math] либо не пересекает полосу [math]\langle a, b \rangle[/math], либо пересекает хотя бы одну из ступенек из множества [math]D[/math].

Лемма:

Если лестница [math]D[/math] полностью соотносима множеству отрезков [math]S[/math], где [math]S[/math] состоит из отрезков, пересекающих полосу [math]\langle a, b \rangle[/math], тогда [math]|S| \le Ends_{a, b}(S) + |Int(D, S)|[/math], где [math]Ends_{a, b}(S)[/math] это число вершин отрезков [math]S[/math], находящихся в пределах полосы [math]\langle a, b \rangle[/math].

Определение:

Если точка [math]p[/math] отрезка [math]s[/math] лежит между ступеньками [math]i[/math] и [math]i + 1[/math], тогда число [math]i[/math] называется местоположением [math]s[/math] на лестнице [math]D[/math] и обозначается как [math]Loc(D, s)[/math]

Утверждение:

Имея лестницу [math]D = (Q, \langle a, b \rangle)[/math] и множество отрезков [math]S[/math], множество [math]Int(D, S)[/math] можно найти за время [math]O(|S| log|Q| + |Int(D, S)|)[/math]. Однако, если [math]S’[/math] упорядочено отношением [math]\lt _x[/math], где [math]x \in [a, b][/math], тогда можно найти [math]Int(D, S)[/math] за время [math]O(|S| + |Q| + |Int(D, S)|)[/math].

Алгоритм

Введем несколько дополнительных функций, чтобы упростить основной алгоритм:

Split

Функция [math]Split[/math] разделяет входное множество отрезков [math]L[/math], пересекающих некоторую полосу [math]\langle a, b \rangle[/math], на подмножества [math]Q[/math] и [math]L'[/math] так, что лестница [math](Q, \langle a, b \rangle)[/math] полностью соотносима множеству отрезков [math]L'[/math].

Пусть [math]L = (s_1 ,..., s_k)[/math], где [math]s_i \lt _b s_{i+1}[/math]
[math]Split_{a,b}(L, Q, L')[/math]
[math]\{[/math]
    [math]L' \leftarrow \varnothing; Q \leftarrow \varnothing[/math]
    for [math]j = 1,...,k[/math] do
        if отрезок [math]S_j[/math] не пересекает
        последний отрезок из [math]Q[/math] внутри полосы [math]\langle a, b \rangle[/math]
        и при этом содержит её then
            добавить [math]s_j[/math] в конец [math]Q;[/math]
        else
            добавить [math]s_j[/math] в конец [math]L’;[/math]
[math]\}[/math]

Эта функция работает за [math]O(|L|)[/math] времени.

Search In Strip

Зная [math]L[/math] мы можем найти [math]Int_{a, b}(L)[/math] и [math]R[/math] используя следующую рекурсивную функцию:

[math]SearchInStrip_{a, b}(L, R)[/math]
[math]\{[/math]
    [math]Split(L, Q, L');[/math] 
    if [math]L' = \varnothing[/math] then
        [math]R \leftarrow Q;[/math] 
        return[math];[/math]
    Найдем [math]Int_{a, b}(Q, L');[/math]
    [math]SearchInStrip_{a, b} (L', R');[/math]
    [math]R \leftarrow Merge_b(Q, R’);[/math]
[math]\}[/math]

Здесь, [math]Merge_x(S_1, S_2)[/math] это функция объединения множеств [math]S_1[/math] и [math]S_2[/math], упорядоченных по отношению [math]\lt _x[/math]. Время выполнения [math]SearchInStrip[/math] эквивалентно сумме времён каждого её запуска. Очевидно, что время работы [math]i[/math]-той функции, будет равно [math]O(|L_i| + |Int_{a, b}(Q_i, {L_i}')|)[/math], где [math]L_i, Q_i, {L_i}'[/math] это соответствующие наборы [math](L_0 = L, L_{i+1} = {L_i}')[/math].

Учитывая лемму, заключаем, что функция [math]SearchInStrip_{a, b}(L, R)[/math] работает за [math]O(|L| + |Int_{a, b}(L)|)[/math].

Предположим, что все отрезки лежат в полосе [math]\langle a, b \rangle[/math]. Таким образом в самом начале у нас есть пара [math](S, \langle a, b, \rangle)[/math]. Что же дальше происходит: множество [math]S[/math] распадается в подмножества [math]Q[/math] и [math]S'[/math], после чего лестница [math]D = (Q, \langle a, b \rangle)[/math] становится полностью соотносимой множеству [math]S'[/math]. Необходимо найти пересечения отрезков из [math]D[/math] и [math]S'[/math], затем, все пересечения в [math]S'[/math]. Чтобы найти пересечения отрезков в [math]S'[/math], мы режем полосу [math]\langle a, b \rangle[/math] и множество [math]S'[/math] по вертикале [math]x = c[/math] на полосы [math]\langle a, c \rangle[/math], [math]\langle c, b \rangle[/math] и множества [math]S'_{ls}[/math], [math]S'_{rs}[/math] соответственно, где c является медианой вершин отрезков, между [math]a[/math] и [math]b[/math]. Затем мы рекурсивно вызываем функцию к парам [math](S'_{ls}, \langle a, c \rangle)[/math] и [math](S'_{rs}, \langle c, b \rangle)[/math]. Ключевым является тот факт, что согласно лемме [math]|S'| \le Ends_{a, b}(S') + |Int(D, S')|[/math], таким образом, число дополнительных отрезков, появляющихся после разрезаний пропорционально числу найденных пересечений.

Основной алгоритм

Давайте разберемся с алгоритмом более подробно:

Не умаляя общности, предположим, что все пересечения и вершины отрезков имеют разные абсциссы (в конечном счете, их можно будет отсортировать введением дополнительных свойств). Будем рассматривать целые координаты на промежутке [math][1, 2N][/math]. Пусть [math]p_i[/math] и [math]s(i)[/math] будут координатами вершин [math]i[/math]-того отрезка.(???)

Основная задача нашего алгоритма, это рекурсивная функция [math]TreeSearch[/math]. Мы соединяем каждый вызов функции с узлом некоего двоичного дерева (далее рекурсивное дерево). Мы отмечаем все значения, множества и параметры вызова соответствующим узлом. В результате, мы проанализируем наш алгоритм рекурсивного дерева. Обозначим множество всех вершин рекурсивного дерева за [math]RT[/math], а множество внутренних вершин за [math]V[/math]. (WAT??)

[math]IntersectingPairs(S_v, a, b):[/math]
    Отсортируем [math]2 \cdot N[/math] вершин по координатам и
        найдем [math]p_i, s(i), i = 1,...,2 \cdot N;\ S_r \leftarrow S_0[/math]
    [math]TreeSearch(S_r, 1, 2 \cdot N)[/math];

[math]TreeSearch(S_r, a, b):[/math]
[math]\{[/math]
    if [math]b - a = 1[/math] then
    [math]\{[/math]
        [math]L \leftarrow[/math] отсортируем [math]S_v[/math] по отношению [math]\lt _b[/math];
        [math]SearchInStrip_{a, b}(L_v, R_v)[/math]; 
        return;
    [math]\}[/math]
    Разделим [math]S_v[/math] на [math]Q_v[/math] и [math]S_v'[/math] так, что лестница
        [math]D_v := (Q_v, \langle a, b \rangle)[/math] будет полностью соотносима множеству [math]S_v'[/math];
    Найдем [math]Int(D_v, S_v')[/math];
    [math]c := \lfloor (a + b)/2 \rfloor[/math];
    Разделим отрезки из [math]S_v'[/math] на пересекающих
        полосу [math]\langle a, c \rangle[/math] [math]S_{ls}(v)[/math] и
        полосу [math]\langle c, b \rangle[/math] [math]S_{rs}(v)[/math];
    [math]TreeSearch(S_{ls}(v), a, c)[/math];
    [math]TreeSearch(S_{rs}(v), c, b)[/math];
[math]\}[/math]

Отсюда и дальше [math]ls(v)[/math], [math]rs(v)[/math] и [math]ft(v)[/math] означают, соответственно, левого сына, правого сына, и отцовскую вершину узла [math]v[/math].

Литература

Т.Вознюк, В.Терещенко — К построению эффективного решения задачи пересечения отрезков
Ф.Препарата, М.Шеймос — Вычислительная геометрия