Использование обхода в глубину для поиска точек сочленения — различия между версиями
м |
|||
| Строка 1: | Строка 1: | ||
| − | = Алгоритм = | + | == Алгоритм == |
Дан [[Отношение связности, компоненты связности|связный]] [[Основные определения теории графов|неориентированный граф]]. Требуется найти все [[Точка сочленения, эквивалентные определения|точки сочленения]] в нем. | Дан [[Отношение связности, компоненты связности|связный]] [[Основные определения теории графов|неориентированный граф]]. Требуется найти все [[Точка сочленения, эквивалентные определения|точки сочленения]] в нем. | ||
| Строка 27: | Строка 27: | ||
<br clear="all"> | <br clear="all"> | ||
| − | = Реализация = | + | == Реализация == |
dfs(<tex>u</tex>, <tex>prev</tex>) | dfs(<tex>u</tex>, <tex>prev</tex>) | ||
| Строка 56: | Строка 56: | ||
Время работы алгоритма совпадает с [[Обход в глубину, цвета вершин#Время работы|временем работы]] <tex> dfs </tex>. | Время работы алгоритма совпадает с [[Обход в глубину, цвета вершин#Время работы|временем работы]] <tex> dfs </tex>. | ||
| − | = Источники = | + | == Источники == |
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр. | Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр. | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Обход в глубину]] | [[Категория: Обход в глубину]] | ||
Версия 10:52, 16 ноября 2013
Алгоритм
Дан связный неориентированный граф. Требуется найти все точки сочленения в нем.
| Теорема: |
Пусть — дерево обхода в глубину, — корень . Вершина — точка сочленения — сын : из или любого потомка вершины нет обратного ребра в предка вершины . — точка сочленения имеет хотя бы двух сыновей в дереве поиска в глубину. |
| Доказательство: |
|
|
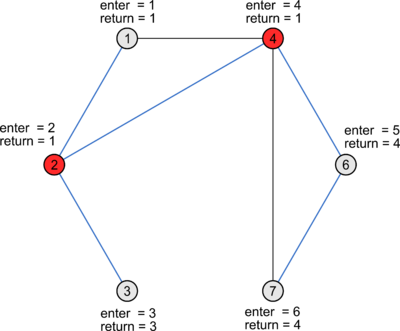
Пусть — время входа поиска в глубину в вершину . Через обозначим минимум из времени захода в саму вершину , времен захода в каждую из вершин , являющуюся концом некоторого обратного ребра , а также из всех значений для каждой вершины , являющейся непосредственным сыном в дереве поиска.
Тогда из вершины или её потомка есть обратное ребро в её предка такой сын , что .
Таким образом, если для текущей вершины существует непосредственный сын : , то вершина является точкой сочленения, в противном случае она точкой сочленения не является.
Реализация
dfs(, ) Помечаем вершину , как посещенную ++ 0 for ( : из ) if ( родитель ) Переходим к следующей итерации цикла if ( посещено) // — предок вершины , — обратное ребро else // — ребенок вершины ++ dfs() if ( >= ) if ( корень) main() ... for ( из ) if ( не посещен) dfs(, -1);
Время работы алгоритма совпадает с временем работы .
Источники
Асанов М., Баранский В., Расин В. - Дискретная математика: Графы, матроиды, алгоритмы — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001, 288 стр.