Эвристики для поиска кратчайших путей

Данная статья - перевод выступления Renato F. Werneck в Microsoft Data Structures and Algorithms School в 2010 году.

Проблема поиска кратчайшего пути

Дано:

• ориентированный граф [math]G=(V,E)[/math]
• [math]l(u,v) \geqslant 0[/math]
• [math]|V|=n, |E|=m[/math]
• отправная точка - вершина [math]s[/math], пункт назначения - вершина [math]t[/math]

Цель: найти кратчайший путь [math] s \rightsquigarrow t[/math]

Мы будем рассматривать сеть автомобильных дорог:

• [math]V[/math] - множество перекрёстков
• [math]E[/math] - множество дорог
• [math]l(u,v)[/math] - среднее время, которое занимает проезд по дороге

Алгоритм Дейкстры

основная статья: Алгоритм Дейкстры

• на каждом шаге выбирает из множества непросмотренных вершин вершину с наименьшим расстоянием до старта и релаксирует рёбра, исходящие из неё
• завершает свою работу, когда цель достигнута (или просмотрены все вершины)

Скорость работы алгоритма Дейкстры сильно зависит от скорости операций с приоритетной очередью.

Поскольку мы рассматриваем сеть автомобильных дорог, то [math]m = O(n)[/math] (граф планарен почти везде).

Для фибоначчиевых куч время работы алгоритма составляет [math]O(V\log{V}+E)[/math], для двоичных куч: [math]O(E\log{V})[/math]

Но на практике чаще используются 2-, 4- и 8-ичные кучи: они более простые, оценка времени работы содержит меньшее количество скрытых констант.

Улучшения алгоритма Дейкстры

Многоуровневые корзины (multi-level buckets, MLB)

Сравнение различных структур данных для поиска кратчайшего пути на карте Европы (CPU 2,4GHz, 16MB RAM)

Структура данных	Время работы (сек)
Двоичная куча	12,38
4-куча	11,53
8-куча	11,52
MLB	9,36
MLB + калибровка	8,04

Подходит только графов с целочисленными рёбрами.

• Будем складывать вершины в "корзины" [math]B[i] \subset V: {d(u)=i} [/math]
• Наша структура данных будет поддерживать индекс [math]L: \forall B[i]: i\lt L \Rightarrow B[i] = \emptyset [/math]
• На каждом шаге алгоритма, если [math]B[L][/math] пусто, то увеличим [math]L[/math], а иначе достанем одну вершину из [math]B[L][/math]
• При релаксации будем убирать вершину из исходной корзины и класть в корзину, соответствующую новому значению [math]dist(u)[/math]

Можно заметить, что при такой реализации, все операции с приоритетной очередью будут выполняться за [math]O(1)[/math]. Тогда, для одного уровня корзин время работы алгоритма Дейкстры можно оценить как [math]O(m+nC)[/math], где [math]C[/math] - максимальная длина ребра в графе.

При двухуровневой реализации будем поддерживать два уровня корзин: первый уровень будет соответствовать одноуровневой реализации, а корзины второго уровня будут содержать диапазон значений корзин первого уровня, которые в них входят.

Соответственно, нам нужно поддерживать два индекса [math]L_{top}[/math] и [math]L_{bottom}[/math] для каждого из уровней соответственно.

При такой реализации, время работы алгоритма Дейкстры можно оценить как [math]O(m+n(1+ \sqrt{C}))[/math]

Калибровка (caliber)

Введём величину калибр (caliber) вершины [math]c(v)[/math] - вес минимального ребра, входящего в [math]v[/math] , или [math]\infty[/math], если в вершину не входит ни одно ребро. Будем говорить, что текущее значение [math]d(v)[/math] точно, если оно равно длине пути [math]s \rightsquigarrow v[/math].

Лемма (1):

Предположим, что длины рёбер неотрицательны. Пусть [math]\mu[/math] - минимальное из текущих значений [math]d(v):v \in V[/math]. Тогда, если существует такая вершина [math]u[/math], что [math]\mu + c(u) \geqslant d(u)[/math], то текущее значение [math]d(u)[/math] точно.

Эта лемма позволяет нам смягчить правило выбора текущей вершины в алгоритме Дейкстры, при этом сохраняя инвариант(почти все вершины обрабатываются единожды). Калибровка использует Лемму 1 чтобы находить и обрабатывать вершины с точными текущими значениями расстояния до них.

Модифицируем нашу MLB - структуру: будем хранить помеченные вершины в двух группах: сет [math]F[/math] и приоритетная очередь [math]B[/math], реализованная на MLB. Алгоритм, приведённый ниже, называется алгоритмом умной очереди (smart queue).

Вершины в [math]F[/math] будут иметь точные метки. Если [math]F[/math] непусто, мы удалим оттуда вершину и прорелаксируем всех её соседей. Если же [math]F[/math] пусто, мы достанем из [math]B[/math] вершину с минимальной меткой и прорелаксируем всех её соседей.

Рассмотрим механизм релаксации: пусть мы уменьшаем [math]d(u)[/math]. Заметим, что в этом случае [math]u[/math] не могло лежать в [math]F[/math](иначе [math]d(u)[/math] было не точно). Если [math]u \in B[/math] - применим [math]decrease - key[/math] к [math]u[/math]. Эта операция либо переместила [math]u[/math] внутри [math]B[/math], либо определила, что метка [math]d(u)[/math] точна и переместила [math]u[/math] в [math]F[/math]. Если же [math]u \notin F \hspace{2 mm} \& \hspace{2 mm} u \notin B[/math], мы применим операцию [math]insert[/math], и [math]u[/math] запишется в [math]F[/math] или [math]B[/math], в зависимости от того, выполняется ли условие леммы.

Двунаправленный поиск

Мы можем уменьшить количество посещённых вершин в алгоритме Дейкстры, просто запустив его и из начальной и из конечной вершины. Такая эвристика не испортит скорость работы в худшем случае.

Создадим две приоритетных очереди и запустим на одной из них алгоритм Дейкстры, ищущий [math]d_{forward}(v)[/math] из [math]s[/math], а на другой - ищущий [math]d_{reverse}(v)[/math] из [math]t[/math]. Алгоритм завершит свою работу, когда какая-нибудь вершина [math]z[/math] будет удалена из обоих очередей.

Тонкость этого алгоритма заключается в том, что кратчайший путь [math]s \rightsquigarrow t[/math] не обязательно пройдёт через вершину [math]v[/math]. Поэтому после остановки двунаправленного поиска, нам необходимо перебрать все рёбра из вершин, имеющих [math]d_{forward}[/math] в вершины с [math]d_{reverse}(v)[/math] и найти ребро [math]uv[/math] с минимальным [math]d_{forward}(u)+\ell(uv)+ d_{reverse}(v) [/math]. Если эта величина меньше, чем длина первоначально найденного пути - то это и есть результат работы алгоритма.

На практике, такой двунаправленный поиск быстрее обычного алгоритма Дейкстры примерно в два раза.

Алгоритм A*

основная статья: Алгоритм A*

Приведём немного изменённую версию этого алгоритма.

Возьмём функцию [math]h(v): V \rightarrow \mathbb{R} [/math] - потенциал (potential) вершины. Тогда, с её помощью можно определить потенциальную стоимость (reduced cost) каждого ребра как [math]\ell_{h}(v,w) = \ell(v,w)-h(v)+h(w)[/math]

Заметим, что замена [math]\ell[/math] на [math]\ell_{h}[/math] не изменит кратчайших путей: возьмём любой путь [math]P = (s=v_{0},v_{1},...,v_{k},v_{k+1}=t)[/math]. Тогда [math]\ell_{h}(P) = \ell_{h}(s,v_{1}), \ell_{h}(s,v_{w})[/math]. Тогда [math]\ell_{h}(P) = \ell_{h}(s,v_{1})+\ell_{h}(v_{1},v_{2})+...+\ell_{h}(v_{k},t) =[/math] [math] \ell(s,v_{1})-h(s)+h(v_{1})+\ell(v_{1},v_{2})-h(v_1)+h(v_{2})+...+\ell(v_{k},t)-h(v_k)+h(t) = [/math] [math]\ell(P)-h(s)+h(t)[/math].

Таким образом длины все путей [math]s \rightsquigarrow t[/math] изменятся на одну и ту же величину [math]h(t)-h(s)[/math]

В нашем случае, алгоритм A* будет эквивалентен алгоритму Дейкстры, на графе [math]G_{h}[/math], у которого стоимости рёбер заменили на их потенциальные стоимости. На каждом шаге необходимо будет выбирать из очереди вершину [math]v[/math] с минимальным значением [math]\ell(P_{s \rightsquigarrow v})-h(s)+h(v)[/math]. Очевидно, [math]h(s)[/math] будет одинаковым для любой вершины [math]v[/math].

Назовём функцию [math]h[/math] правдоподобной (feasible), если [math]\forall (u,v): \ell_{h}(u,v) \geqslant 0[/math]. Известно, что, если [math]h(t)\leqslant 0[/math] и [math]h[/math] правдоподобна, то для любого [math]v[/math], [math]h(v)[/math] - нижняя граница [math]dist(v,t)[/math]

Главное отличие от алгоритма Дейкстры в том, что A* является информированным алгоритмом - он обрабатывает в первую очередь те вершины, которые находятся ближе к результату.

Скорость работы алгоритма A*:

• в худшем случае - [math]h(v)=0[/math] - вырождается в алгоритм Дейкстры
• в лучшем случае - [math]\forall v: h(v)=dist(v,t)[/math]
  • [math]\ell_{h}(v,w)=0[/math], если ребро [math](v,w)[/math] лежит на кратчайшем пути, иначе потенциальная стоимость положительна
  • все посещённые вершины будут лежать на кратчайшем пути

Двунаправленный A*

Для двунаправленной версии алгоритма нам нужны две потенциальные функции:

• [math]p_{f}(v)[/math], оценивающая [math]dist(v,t)[/math]
• [math]p_{r}(v)[/math], оценивающая [math]dist(s,v)[/math]

В этом случае появляется дополнительная проблема: различные потенциальные стоимости у рёбер для различных обходов:

• [math]\ell_{p_{f}}(v,w) = \ell(v,w)-p_{f}(v)+p_{f}(w)[/math] - если ребро обрабатывается в обходе, начатом в [math]s[/math]
• [math]\ell_{p_{r}}(v,w) = \ell(v,w)-p_{r}(w)+p_{r}(v)[/math] - если ребро обрабатывается в обходе, начатом в [math]t[/math]

Чтобы избежать этой проблемы, необходимо, чтобы [math]\ell_{p_{f}}(v,w) = \ell_{p_{r}}(v,w) \Leftrightarrow p_{f}(v) + p_{r}(v) = p_{f}(w) + p_{r}(w) = const[/math]. Кроме того, функции должны бить монотонными.

Решение - использовать усреднённые потенциальные функции:

• [math]h_{f}(v) = \frac{p_{f}(v)-p_{r}(v)}{2}[/math]
• [math]h_{r}(v) = \frac{p_{r}(v)-p_{f}(v)}{2} = -h_{f}(v)[/math]

При таком выборе потенциальных функций, выполняется [math]\forall u : h_{f}(u)+h_{r}(u)=0[/math] и тогда двунаправленный A* становится аналогичен двунаправленному алгоритму Дейкстры

Двухэтапные алгоритмы

К сожалению, двунаправленный алгоритм Дейкстры всего в два раза быстрее обычного, а это слишком медленно. Рассмотрим алгоритм поиска кратчайшего пути, состоящий из двух этапов:

1. Препроцессинг
   • запускается единожды для графа
   • может занимать много времени
   • рассчитывает некую вспомогательную информацию
2. Запрос
   • может использовать данные, полученные во время препроцессинга
   • запускается по требованию для пары [math](s,t)[/math]
   • должен выполняться очень быстро (в реальном времени)

Можно рассмотреть в этом ключе два примера:

• Алгоритм Дейкстры: препроцессинг - ничего не делать, запрос - выполнение алгоритма Дейкстры;
• Полный перебор: препроцессинг - посчитать таблицу расстояний размером [math]n \times n[/math] (займёт порядка 5 лет времени и 1 петабайта памяти для карты Европы), запрос - обратиться к элементу таблицы.

Оба эти примера - крайние случаи. Нам нужно нечто более гибкое: препроцессинг за часы/минуты, рост количества предпосчитанных данных линейно от размера графа и запросы в реальном времени.

ALT

Аббревиатура ALT расшифровывается как A* +Landmarks + Triangle inequality : A* + ориентиры + неравенство треугольника.

Препроцессинг:

• взять небольшое количество вершин (например, 16), обозначив их как ориентиры (landmarks)
• для каждого из ориентиров посчитать кратчайшие пути до всех вершин
• сохранить эти пути

Запрос:

• используем A*
• если некоторое ребро находится на кратчайшем пути между исходной точкой и ориентиром - по нему идём в первую очередь

Будем использовать неравенство треугольника для нижних оценок пути:

• [math]dist(v,w)\ge dist(A,w)-dist(A,v)[/math]
• [math]dist(v,w)\ge dist(v,A)-dist(w,A)[/math]
• [math]dist(v,w)\ge max\{dist(A,w)-dist(A,v),dist(v,A)-dist(w,A)\}[/math]

Эта эвристика хорошо работает, на дорожных графах, для которых верно следующее: как правило, кратчайший путь затрагивает небольшое количество локальных дорог, потом крупную автомагистраль и снова некоторое количество локальных дорог.

Выбор ориентиров

Сложности в выборе ориентиров:

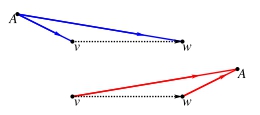
• хороший ориентир для запроса [math]s \rightsquigarrow t[/math] должен находиться "до" [math]s[/math] (точно не будет общих рёбер на кратчайшем пути) или "за" [math]t[/math] (чем острее угол, тем меньше отклонение от предварительно посчитанного кратчайшего пути до искомого)
• Нам нужно выбрать такие ориентиры, которые будут неплохими для всех запросов.

Выглядит логичным выбирать ориентиры на краю дорожной сети.

Существуют различные способы выбора ориентиров:

Случайный выбор (random)

Как следует из названия, ориентиры выбираются случайным образом

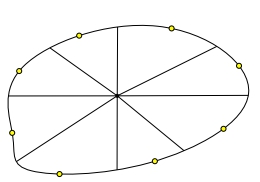
Плоскостной (planar)

• разделим карту на [math]k[/math] секторов одинаковой площади
• возьмём ориентиром наиболее удалённую точку от центра в каждом секторе

Такой способ подходит, только если граф имеет относительно правильную форму. На практике обычно используется оптимизированная версия этого алгоритма.

Ссылки

• Википедия:Алгоритм_поиска_A*
• Wikipedia:A*_search_algorithm
• Статья о поиске кратчайших путей
• Generalized best-first search strategies and the optimality of A*