Числа Эйлера I и II рода — различия между версиями
VolhovM (обсуждение | вклад) (→Вывод рекуррентной формулы) |
VolhovM (обсуждение | вклад) (→Вывод рекуррентной формулы) |
||
| Строка 10: | Строка 10: | ||
1. Количество подъемов в перестановке <tex dpi = "130">\theta</tex> равно количеству подъемов в <tex dpi = "130">\pi</tex>. Этого можно добиться, вставляя элемент <tex dpi = "130">n</tex> на самое первое место в <tex dpi = "130">\theta</tex> (всего <tex dpi = "160">\langle{n\atop m}\rangle </tex> возможностей) или перед последним последним элементом каждого подъема (еще <tex dpi = "130">m \times </tex><tex dpi = "160"> \langle{n\atop m}\rangle </tex> раз). | 1. Количество подъемов в перестановке <tex dpi = "130">\theta</tex> равно количеству подъемов в <tex dpi = "130">\pi</tex>. Этого можно добиться, вставляя элемент <tex dpi = "130">n</tex> на самое первое место в <tex dpi = "130">\theta</tex> (всего <tex dpi = "160">\langle{n\atop m}\rangle </tex> возможностей) или перед последним последним элементом каждого подъема (еще <tex dpi = "130">m \times </tex><tex dpi = "160"> \langle{n\atop m}\rangle </tex> раз). | ||
| − | 2. Количество подъемов в новой перестановке на один больше предыдущего количества. Этого эффекта добиваемся вставкой элемента <tex dpi = "130">n</tex> | + | 2. Количество подъемов в новой перестановке на один больше предыдущего количества. Этого эффекта добиваемся вставкой элемента <tex dpi = "130">n</tex> во все места, не подходящие по критерию первого пункта. Таких вставок, как не трудно догадаться, можно совершить <tex dpi = "130">(n - m)</tex><tex dpi = "160">\langle{n\atop m}\rangle</tex>. |
Тогда рекуррентная формула имеет вид: | Тогда рекуррентная формула имеет вид: | ||
| Строка 21: | Строка 21: | ||
Также для четных <tex dpi = "130">k</tex>: | Также для четных <tex dpi = "130">k</tex>: | ||
| − | :<tex dpi = "160">\left\langle{n\atop m}\right\rangle = [ | + | :<tex dpi = "160">\left\langle{n\atop m}\right\rangle = [m = 0]</tex>, |
Запись [выражение] означает нотацию Айверсона, где | Запись [выражение] означает нотацию Айверсона, где | ||
:<tex dpi = "160"> [statement] =</tex><tex dpi = "140"> \begin{cases} 1 & \text{statement} \\ 0 & \text{!statement} \end{cases}</tex> | :<tex dpi = "160"> [statement] =</tex><tex dpi = "140"> \begin{cases} 1 & \text{statement} \\ 0 & \text{!statement} \end{cases}</tex> | ||
Версия 02:04, 19 декабря 2013
Числа Эйлера I рода (Eulerian numbers) — количество перестановок чисел от 1 до n таких, что в каждой из них существует ровно m подъемов. Числа Эйлера I рода обозначают как или же .
| Определение: |
| Пусть и - элементы некоторой перестановки порядка причем . Тогда пара называется подъемом (ascent) данной перестановки. |
Содержание
Вывод рекуррентной формулы
Пусть у нас есть некая перестановка . Тогда операцией вставки элемента с номером n в какую-либо из позиций мы получим перестановок вида . Далее рассмотрим два случая:
1. Количество подъемов в перестановке равно количеству подъемов в . Этого можно добиться, вставляя элемент на самое первое место в (всего возможностей) или перед последним последним элементом каждого подъема (еще раз).
2. Количество подъемов в новой перестановке на один больше предыдущего количества. Этого эффекта добиваемся вставкой элемента во все места, не подходящие по критерию первого пункта. Таких вставок, как не трудно догадаться, можно совершить .
Тогда рекуррентная формула имеет вид:
Примем также следующие начальные значения:
- , если
Также для четных :
- ,
Запись [выражение] означает нотацию Айверсона, где
Пример
Рассмотрим все перестановки порядка , в которых есть ровно 2 подъема (в квадратных скобках один или больше подъемов подряд):
Согласно алгоритму вывода рекуррентной формулы мы можем добавить '4' в следующие позиции всех перестановок порядка с двумя подъемами, не увеличив количество подъемов:
Далее рассмотрим все перестановки порядка с одним подъемом, причем операцией вставки мы будем увеличивать количество перестановок на 1:
Таким образом мы убеждаемся в верности формулы:
Треугольник чисел Эйлера I рода и явная формула
Явная формула
Приведем также без вывода явную формулу для вычисления чисел Эйлера I рода:
Треугольник чисел Эйлера I рода
На значениях чисел Эйлера I рода можно построить массив , нижнедиагональная часть которого названа треугольником чисел Эйлера I рода.
m = 0 1 2 3 4 5 6 7 8 9 10 11 12 n = 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 2 1 1 0 0 0 0 0 0 0 0 0 0 0 3 1 4 1 0 0 0 0 0 0 0 0 0 0 4 1 11 11 1 0 0 0 0 0 0 0 0 0 5 1 26 66 26 1 0 0 0 0 0 0 0 0 6 1 57 302 302 57 1 0 0 0 0 0 0 0 7 1 120 1191 2416 1191 120 1 0 0 0 0 0 0 8 1 247 4293 15619 15619 4293 247 1 0 0 0 0 0 9 1 502 14608 88234 156190 88234 14608 502 1 0 0 0 0 10 1 1013 47840 455192 1310354 1310354 455192 47840 1013 1 0 0 0 11 1 2036 152637 2203488 9738114 15724248 9738114 2203488 152637 2036 1 0 0 12 1 4083 478271 10187685 66318474 162512286 162512286 66318474 10187685 478271 4083 1 0
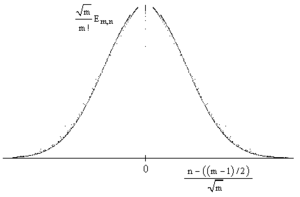
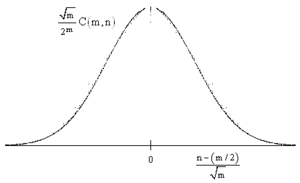
Стоит отметить, что гистрограмма, построенная на значениях чисел Эйлера I рода аппроксимируется к гистограмме, построенной на биноминальных коээфициентах (оба графика, представленные справа, смасштабированы; масштаб указан на гистограмме):
Полезные факты о числах Эйлера I рода
1. Нетрудно увидеть, что каждый ряд ненулевых значений симметричен относительно своей середины, то есть:
2. Сумма всех значений каждого ряда равна :
3. Еще одно условие равенства нулю:
Числа Эйлера II рода
Числа Эйлера II рода(Eulerian numbers of the second kind) — количество перестановок мультимножества от до вида , обладающих свойством "все элементы перестановки, встречающиеся между двумя вхождниями для любого , больше, чем ", таких, что в каждой из них существует ровно подъемов. Числа Эйлера II рода обозначаются как
Пример
Рассмотрим . Тогда существует 15 перестановок такого вида, среди которых одна не имеет подъемов, 8 штук имеют всего 1 подъем, и 6 перестановок имеют 2 подъема:
| Лемма: |
Количество перестановок мультимножества со свойством "все элементы перестановки, встречающиеся между двумя вхождниями для любого , больше, чем
" равно двойному факториалу . |
Рекурсивная формула
Числа Эйлера II рода можно выразить рекурсивно следующим образом:
С начальным условием для :
Треугольник чисел Эйлера II рода
Значения чисел Эйлера II рода представлены в данном массиве. Нижнедиагональная его часть называется треугольником чисел Эйлера II рода.
m = 0 1 2 3 4 5 6 7 8 n = 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 2 1 2 0 0 0 0 0 0 0 3 1 8 6 0 0 0 0 0 0 4 1 22 58 24 0 0 0 0 0 5 1 52 328 444 120 0 0 0 0 6 1 114 1452 4400 3708 720 0 0 0 7 1 240 5610 32120 58140 33984 5040 0 0 8 1 494 19950 195800 644020 785304 341136 40320 0 9 1 1004 67260 1062500 5765500 12440064 11026296 3733920 362880