Хроматическое число планарного графа — различия между версиями
Martoon (обсуждение | вклад) м |
Martoon (обсуждение | вклад) м |
||
| Строка 6: | Строка 6: | ||
|statement=В любом графе <tex> G </tex> существует вершина степени не больше 5 | |statement=В любом графе <tex> G </tex> существует вершина степени не больше 5 | ||
|proof= | |proof= | ||
| − | Предположим это не так. Для любой вершины <tex> u_i </tex> графа <tex> G </tex> верно <tex> \mathrm{deg} | + | Предположим это не так. Для любой вершины <tex> u_i </tex> графа <tex> G </tex> верно <tex> \mathrm{deg} \ u_i \ge 6 </tex>. Если сложить это неравенство для всех <tex> i </tex>, получим <tex> 2E \ge 6V </tex>. Но по [[Формула_Эйлера#EulerFormulaCons|следствию из теоремы Эйлера]] <tex> E \le 3V-6 </tex>. Пришли к противоречию. |
}} | }} | ||
Версия 19:47, 22 декабря 2013
Для планарного графа можно дать оценку сверху на хроматическое число.
Раскраска в 6 цветов
| Лемма: |
В любом графе существует вершина степени не больше 5 |
| Доказательство: |
| Предположим это не так. Для любой вершины графа верно . Если сложить это неравенство для всех , получим . Но по следствию из теоремы Эйлера . Пришли к противоречию. |
| Теорема: |
Пусть граф - планарный. Тогда |
| Доказательство: |
|
Докажем по индукции.
Если граф содержит не более 6 вершин, то утверждение очевидно.
Предположим, что для планарного графа с вершинами существует раскраска в 6 цветов. Докажем то же для графа с вершиной. По только что доказанной лемме в найдётся вершина степени не больше 5. Удалим её; по предположению индукции получившийся граф можно раскрасить в 6 цветов. Вернём удалённую вершину и покрасим её в цвет, не встречающийся среди смежных ей вершин. Индукционный переход доказан |
Раскраска в 5 цветов
| Теорема: |
Пусть граф - планарный. Тогда |
| Доказательство: |
|
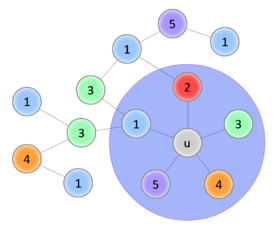
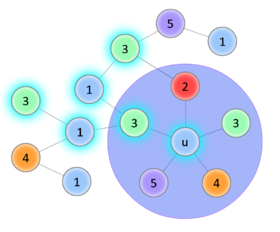
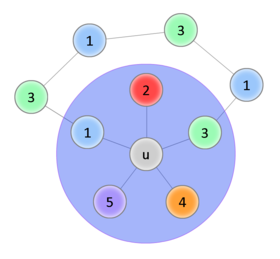
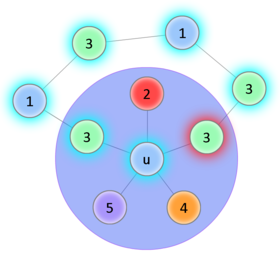
Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Покажем что для случая с 5-ю цветами всё равно можно вернуть удалённую вершину так, чтобы раскраска осталась правильной. Обозначим за - возвращаемую вершину, - вершина, покрашенная в цвет. Если среди вершин, смежных , есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим . Иначе, уложим полученный после удаления граф на плоскость и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке. Попробуем покрасить в цвет 1. Чтобы раскраска осталась правильной, перекрасим смежную ей вершину в цвет 3. Если среди смежных ей вершин есть вершины , покрасим их в цвет 1, и так далее. Рассмотрим две необычные ситуации, которые могут наступить во время обхода:
Если этот процесс был успешно завершён, то получили правильную раскраску. Если же в соответствии со 2-ым вариантом перекраска не удалась, это означает, что в есть цикл . Тогда попытаемся таким же образом перекрасить в цвет 2, а смежную ей в цвет 4 (со последующими перекрасками). Если удастся - раскраска получена. Если нет, то получили ещё один цикл . Но граф планарный, значит два полученных цикла пересекаются по крайней мере в двух вершинах - и какой-то другой, что невозможно, ведь вершины первого цикла и второго - разных цветов. Значит такой случай наступить не мог. |
| Успешное перекрашивание | |
 |
|
| Цикл 1-3, перекрасить не удаётся | |
 |
|
Заметим что нельзя составить подобное доказательство для раскраски в 4 цвета, поскольку здесь наличие двух вершин одного цвета среди смежных не исключает того, что все они раскрашены в разные цвета
Раскраска в 4 цвета
Данная теорема была доказана Кеннетом Аппелем и Вольфгангом Хакеном. Их доказательство сводилось к рассмотрению порядка 2000 графов, 4-раскрашиваемость которых была проверена при помощи компьютера. Подробнее см. здесь.