ППЛГ и РСДС (PSLG и DCEL): определение, построение РСДС множества прямых

Представление плоского графа с помощью РСДС

Плоский граф, ребрам которого придана произвольная ориентация для представления его с помощью РСДС. Стрелки вокруг вершин соответствуют указателям (P1, P2)

(а) РСДС, (б) входы по вершинам head_V [1..n] и (в) входы по граням head_F[1..l]

ППЛГ — Плоский прямолинейный планарный граф.

РСДС — Реберный список с двойными связями.

ППЛГ

Планарный граф, уложенный на плоскости, принято называть плоским. Плоская укладка планарного графа [math]G = (V, E)[/math] — это отображение каждой вершины из [math]V[/math] в точку на плоскости, а каждого ребра из [math]E[/math] в простую линию, соединяющую пару образов концевых вершин этого ребра так, чтобы образы ребер пересекались только в своих концевых точках. Хорошо известно, что любой планарный граф можно уложить на плоскости так, чтобы все ребра отобразились в прямолинейные отрезки.

РСДС

Первое описание

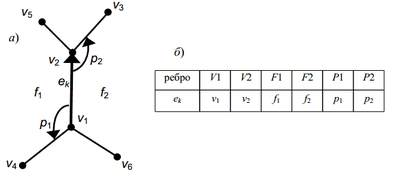
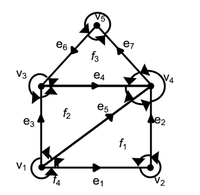
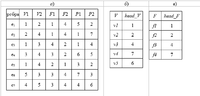
Реберный список с двойными связями особенно удобен для представления ППЛГ. Пусть задан граф [math]G = (V, E)[/math], [math]V = \{v_1, v_2... v_n\}[/math], а [math]E = \{e_1, e_2... e_n\}[/math]. Главная компонента РСДС для планарного графа это реберный узел. Между ребрами графа и реберными узлами РСДС существует взаимно однозначное соответствие, т.е. каждое ребро представлено в РСДС ровно один раз. Реберный узел РСДС, соответствующий ребру графа, например, [math]e_k = \{v_1, v_2\} [/math] имеет 4 поля ([math]V1, V2, F1, F2[/math]) и 2 указателя ([math]P1, P2[/math]). Поле [math]V1[/math] содержит начало ребра, а поле [math]V2[/math] содержит его конец (так изначально неориентированное ребро получает условную ориентацию). Поля [math]F1[/math] и [math]F2[/math] содержат имена граней, лежащих слева и справа от ориентированного ребра ([math]v_1, v_2[/math]). Указатель [math]P1[/math] (соответственно [math]P2[/math]) задает реберный узел, содержащий первое ребро, встречаемое вслед за ребром ([math]v_1, v_2[/math]), при повороте от него против часовой стрелки вокруг [math]v_1[/math] (соответственно [math]v_2[/math]).

Ко второму описанию

Второе описание

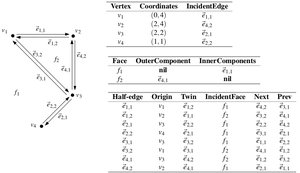
РСДС состоит из 3 компонент:

• Vertex — это точка сочленения. Содержит координаты точки. А так же указатель на инцидентное ребро.
• Face — содержит указатель на наружную компоненту (некоторое ребро на его границе). Для неограниченных поверхностей это nil. Так же содержит внутреннюю компоненту, которая есть указатель на некое ребро, с которого можно начать описывать внутреннюю область (опять же, может быть nil).
• Half-edge — это ребро. Содержит указатели на точку, откуда исходит (origin), указатель на ребро близнец (twin)(направленное в другую сторону), инцидентную поверхность (incident_face), и указатели на следующее и предыдущие ребра.

struct vertex {
    x, y;
    half_edge *rep;  /* rep->origin == this */
};

struct face {
    outer_component *out;
    inner_component *in;
};

struct half_edge {
    half_edge *prev;  /* prev->next == this */
    half_edge *next;  /* next->prev == this */
    half_edge *twin;  /* twin->twin == this */
    vertex *origin;     /* twin->next->origin == origin &&
                                prev->twin->origin == origin */
    face *incident_face;       /* prev->incident_face == incident_face && next->incident_face == incident_face */
};

Построение РСДС множетсва прямых

Алгоритм: Для каждой конечной точки создаем vertex. Для каждого входного сегмента создаем 2 half-edge и присваиваем vertex в origin и создаем поля twin. Для каждой конечной точки сортируем (по часовой стрелке) half-edge, у которых origin vertex и есть эта точка. Для каждой пары half-edge e1, e2, по часовой стрелке присваиваем e1->twin->next = e2 и e2->prev = e1->twin. Выбираем один из этих half-edge и делаем его представителем точки. (Вырожденный случай: если есть только 1 half-edge в отсортированном списке, то присваиваем e->twin->next = e и e->prev = e->twin. Если сделать четко, то это не понадобится). Следующие указатели это перестановки half-edge. В каждом цикле находим и создаем face.