Skip quadtree: определение, время работы — различия между версиями
Gromak (обсуждение | вклад) |
Gromak (обсуждение | вклад) |
||
| Строка 6: | Строка 6: | ||
Skip quadtree {{---}} как skip list, только вместо list'а quadtree. Поэтому желательно знать, что такое [[Список с пропусками | skip list]], и необходимо знать, что такое [[Квадродеревья и перечисление точек в произвольном прямоугольнике (статика)#Сжатое квадродерево | сжатое квадродерево]]. В данной статье будет рассматриваться только рандомизированая версия этой структуры, потому что больше и не нужно, кажется. | Skip quadtree {{---}} как skip list, только вместо list'а quadtree. Поэтому желательно знать, что такое [[Список с пропусками | skip list]], и необходимо знать, что такое [[Квадродеревья и перечисление точек в произвольном прямоугольнике (статика)#Сжатое квадродерево | сжатое квадродерево]]. В данной статье будет рассматриваться только рандомизированая версия этой структуры, потому что больше и не нужно, кажется. | ||
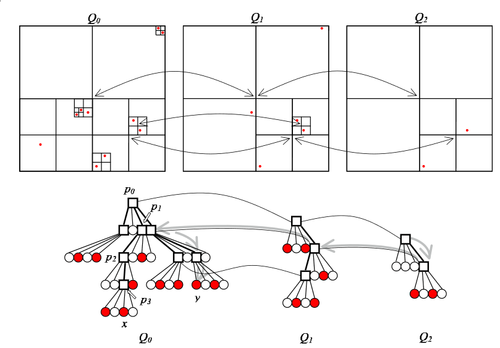
| − | The randomized skip quadtree {{---}} последовательность сжатых квадродеревьев над последовательностью подмножеств некоего исходного множества <tex>S</tex>. <tex>S_0 = S</tex>, в <tex>S_1</tex> каждый элемент из <tex>S_0</tex> входит с вероятностью <tex>p</tex>. The randomized skip quadtree состоит из последовательности <tex>\{Q_i\}</tex>, где <tex>Q_i</tex> {{---}} сжатое квадродерево над множеством <tex>S_i</tex>. Будем называть эти квадродеревья уровнями, при этом нулевой уровень содержит в точности точки из <tex>S</tex>. | + | The randomized skip quadtree {{---}} последовательность сжатых квадродеревьев над последовательностью подмножеств некоего исходного множества <tex>S</tex>. <tex>S_0 = S</tex>, в <tex>S_1</tex> каждый элемент из <tex>S_0</tex> входит с вероятностью <tex>p</tex> и так далее. The randomized skip quadtree состоит из последовательности <tex>\{Q_i\}</tex>, где <tex>Q_i</tex> {{---}} сжатое квадродерево над множеством <tex>S_i</tex>. Будем называть эти квадродеревья уровнями, при этом нулевой уровень содержит в точности точки из <tex>S</tex>. |
Заметим, что если какой-то квадрат [[Квадродеревья и перечисление точек в произвольном прямоугольнике (статика)#interesting | интересный]] в <tex>Q_i</tex>, то он интересный и в <tex>Q_{i-1}</tex>. | Заметим, что если какой-то квадрат [[Квадродеревья и перечисление точек в произвольном прямоугольнике (статика)#interesting | интересный]] в <tex>Q_i</tex>, то он интересный и в <tex>Q_{i-1}</tex>. | ||
| Строка 12: | Строка 12: | ||
Будем для каждого интересного квадрата на каждом уровне хранить указатели на тот же квадрат уровнем ниже и уровнем выше (если есть). | Будем для каждого интересного квадрата на каждом уровне хранить указатели на тот же квадрат уровнем ниже и уровнем выше (если есть). | ||
| − | Локализация выполняется аналогично сжатому квадродереву. Сначала локализуемся в квадродереве наибольшего уровня, начиная с его корня. Затем локализуемся в квадродереве уровня ниже, начиная уже не с корня, а с того квадрата, который нашли на прошлом уровне. И так далее, пока не дойдём до дна. | + | Локализация выполняется аналогично сжатому квадродереву. Под локализацией под разумевается, что мы хотим найти минимальный интересный квадрат задержащий данную точку (содержит геометрически, в самом дереве её может не быть, тут, возможно, правильнее сказать «пересекает»). Сначала локализуемся в квадродереве наибольшего уровня, начиная с его корня. Затем локализуемся в квадродереве уровня ниже, начиная уже не с корня, а с того квадрата, который нашли на прошлом уровне. И так далее, пока не дойдём до дна. |
| − | Для добавления сначала надо локализоваться. При этом мы локализуемся сразу на всех уровнях. Дальше добавляемся в нулевой уровень, затем с вероятностью <tex>p</tex> добавляемся на уровень выше и так далее до первого недобавления. При этом количество уровней должно увеличиться максимум на 1. | + | Для добавления сначала надо локализоваться. При этом мы локализуемся сразу на всех уровнях (так уж устроен процесс). Дальше добавляемся в нулевой уровень, затем с вероятностью <tex>p</tex> добавляемся на уровень выше и так далее до первого недобавления. При этом количество уровней должно увеличиться максимум на 1, то есть, если появился новый уровень, то процесс точно заканчивается. |
Удаление совсем просто: локализуемся, удаляем со всех уровней, на которых есть. | Удаление совсем просто: локализуемся, удаляем со всех уровней, на которых есть. | ||
== Время работы == | == Время работы == | ||
| + | |||
| + | {{Лемма | ||
| + | |about= | ||
| + | О количестве шагов на одном уровне | ||
| + | |statement= | ||
| + | На каждом уровне совершается <tex>O(1)</tex> шагов поиска. | ||
| + | |proof= | ||
| + | ЫЫЫ | ||
| + | }} | ||
== Источник == | == Источник == | ||
http://arxiv.org/pdf/cs.cg/0507049.pdf | http://arxiv.org/pdf/cs.cg/0507049.pdf | ||
Версия 13:23, 7 января 2014
Описание
Skip quadtree — как skip list, только вместо list'а quadtree. Поэтому желательно знать, что такое skip list, и необходимо знать, что такое сжатое квадродерево. В данной статье будет рассматриваться только рандомизированая версия этой структуры, потому что больше и не нужно, кажется.
The randomized skip quadtree — последовательность сжатых квадродеревьев над последовательностью подмножеств некоего исходного множества . , в каждый элемент из входит с вероятностью и так далее. The randomized skip quadtree состоит из последовательности , где — сжатое квадродерево над множеством . Будем называть эти квадродеревья уровнями, при этом нулевой уровень содержит в точности точки из . Заметим, что если какой-то квадрат интересный в , то он интересный и в .
Операции над skip quadtree
Будем для каждого интересного квадрата на каждом уровне хранить указатели на тот же квадрат уровнем ниже и уровнем выше (если есть).
Локализация выполняется аналогично сжатому квадродереву. Под локализацией под разумевается, что мы хотим найти минимальный интересный квадрат задержащий данную точку (содержит геометрически, в самом дереве её может не быть, тут, возможно, правильнее сказать «пересекает»). Сначала локализуемся в квадродереве наибольшего уровня, начиная с его корня. Затем локализуемся в квадродереве уровня ниже, начиная уже не с корня, а с того квадрата, который нашли на прошлом уровне. И так далее, пока не дойдём до дна.
Для добавления сначала надо локализоваться. При этом мы локализуемся сразу на всех уровнях (так уж устроен процесс). Дальше добавляемся в нулевой уровень, затем с вероятностью добавляемся на уровень выше и так далее до первого недобавления. При этом количество уровней должно увеличиться максимум на 1, то есть, если появился новый уровень, то процесс точно заканчивается.
Удаление совсем просто: локализуемся, удаляем со всех уровней, на которых есть.
Время работы
| Лемма (О количестве шагов на одном уровне): |
На каждом уровне совершается шагов поиска. |
| Доказательство: |
| ЫЫЫ |