Статические выпуклые оболочки: Джарвис, Грэхем, Эндрю, Чен, QuickHull

Конспект не готов.

Ниже приводятся основные алгоритмы построения выпуклых оболочек статического множества. Используются обозначения: [math]n[/math] - размер входных данных, [math]k[/math] - размер оболочки.

Алгоритм Джарвиса

По-другому "Gift wrapping algorithm" (Заворачивание подарка).

Описание Алгоритма

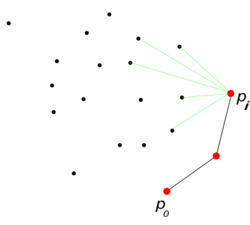
1) Возьмем самую правую нижнюю точку [math]p_0[/math] нашего множества. Добавляем ее в ответ.

2) На каждом следующем шаге для последнего добавленного [math]p_i[/math] ищем [math]p_{i + 1}[/math] среди всех недобавленных точек и [math]p_0[/math] с максимальным полярным углом относительно [math]p_i[/math] (Если углы равны, надо сравнивать по расстоянию). Добавляем [math]p_{i + 1}[/math] в ответ. Если [math]p_{i + 1} == p_0[/math] , заканчиваем алгоритм.

Корректность

Точка [math]p_0[/math], очевидно, принадлежит оболочке. На каждом последующем шаге алгоритма мы получаем прямую [math]p_{i-1}p_i[/math], по построению которой все точки множества лежат слева от нее. Значит, выпуклая оболочка состоит из [math]p_{i}[/math]-ых и только из них.

Псевдокод

Inplace-реализация алгоритма. [math]S[1..n][/math] - исходное множество.

 Jarvis(S)
   find i such that S[i] has the lowest y-coordinate and highest x-coordinate
   p0 = S[i]
   pi = p0
   k = 0
   do 
     k++
     for i = k..n 
       if S[i] has lower angle and higher distance than S[k] in relation to pi
         swap(S[i], S[k])
     pi = S[k]
   while pi != p0
   return k

Сложность

Добавление каждой точки в ответ занимает [math]O(n)[/math] времени, всего точек будет [math]k[/math], поэтому итоговая сложность [math]O(nk)[/math].

Ссылки

• Английская статья — Wikipedia
• Русская статья — Wikipedia

Алгоритм Грэхема

Описание Алгоритма

Промежуточный шаг алгоритма

1)Находим самую правую нижнюю точку множества [math]p_0[/math], добавляем в ответ. 2)Сортируем все остальные точки по полярному углу относительно [math]p_0[/math]. 3)Добавляем в ответ [math]p_1[/math] - самую первую из отсортированных точек. 4)Берем следующую по счету точку в массиве [math]t[/math]. Пока [math]t[/math] и две последних точке в ответе образуют неправый поворот, удаляем из ответа последнюю точку. 5)Делаем п.4, пока не закончатся точки.

Псевдокод

Подаем в функцию исходное множество S, возвращаем позицию [math]k[/math] - в [math]S[1..k - 1][/math] будет хранится наша оболочка. [math]turn(a, b, c)[/math] - модифицированная функция поворота, учитывающая случай, когда точки лежат на одной прямой.

Сложность

Сортировка точек занимает [math]O(n log n)[/math] времени. При обходе каждая точка добавляется в ответ не более одного раза, поэтому сложность этой части - [math]O(n)[/math]. Суммарное время - [math]O(n log n)[/math].