Диаграмма Вороного — различия между версиями
Megabyte (обсуждение | вклад) |
Megabyte (обсуждение | вклад) |
||
| Строка 11: | Строка 11: | ||
Расстояние от точки <tex>x \in \mathbb{E}^2</tex> до замкнутого сайта <tex>S_i</tex>: <tex>\delta(x, S_i) = \min{\{||x - y|| : y \in S_i\}}</tex>. | Расстояние от точки <tex>x \in \mathbb{E}^2</tex> до замкнутого сайта <tex>S_i</tex>: <tex>\delta(x, S_i) = \min{\{||x - y|| : y \in S_i\}}</tex>. | ||
| − | Пусть <tex>H_{ij} = \{x \in \mathbb{E}^2 : \delta(x, S_i) \le \delta(x, S_j)\}</tex>. '''Ячейка Вороного''' (''Voronoi cell'') <tex>V(S_i, \Sigma)</tex> {{---}} множество точек, которые находятся ближе к <tex>S_i</tex>, чем к любому другому сайту, то есть <tex>V(S_i, \Sigma) = \cap_{i \ne j}H_{ij}</tex> | + | Пусть <tex>H_{ij} = \{x \in \mathbb{E}^2 : \delta(x, S_i) \le \delta(x, S_j)\}</tex>. '''Ячейка Вороного''' (''Voronoi cell'') <tex>V(S_i, \Sigma)</tex> {{---}} множество точек, которые находятся ближе к <tex>S_i</tex>, чем к любому другому сайту, то есть <tex>V(S_i, \Sigma) = \cap_{i \ne j}H_{ij}</tex>. |
'''Ребро Вороного''' (''Voronoi edge'') {{---}} связное множество точек, принадлежащих пересечению ровно двух ячеек Вороного. | '''Ребро Вороного''' (''Voronoi edge'') {{---}} связное множество точек, принадлежащих пересечению ровно двух ячеек Вороного. | ||
| Строка 42: | Строка 42: | ||
'''4'''. Обновить локализационную структуру. | '''4'''. Обновить локализационную структуру. | ||
| + | |||
| + | {{Лемма | ||
| + | |statement= | ||
| + | <tex>\Sigma</tex> {{---}} слабо пересекающееся между собой множество сайтов. Тогда <tex>\forall s \in \Sigma</tex> ячейки Вороного <tex>V(s, \Sigma)</tex> {{---}} односвязные множества. | ||
| + | |proof= | ||
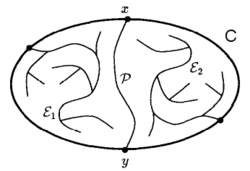
| + | Для начала докажем, что ячейки связны. Пусть это не так и у ячейки <tex>V(s, \Sigma)</tex> несколько компонент связности. Рассмотрим <tex>\varepsilon</tex> {{---}} одну из тех, которая не содержит в себе <tex>s</tex>. Начнём идти по кратчайшему пути <tex>P</tex> от любой точки <tex>p \in \varepsilon</tex> до <tex>s</tex>. Так как <tex>p</tex> и <tex>s</tex> лежат в разных компонентах связности, найдётся <tex>s' \in \Sigma</tex>, такой что путь <tex>P</tex> проходит через <tex>V(s', \Sigma)</tex>. Значит существует путь от <tex>p</tex> до <tex>s'</tex>, который короче, чем <tex>P</tex>, следовательно и <tex>\delta(p, s') < \delta(p, s) = |P|</tex>. Противоречие. | ||
| + | |||
| + | Теперь допустим, что <tex>V(s, \Sigma)</tex> содержит разрыв в виде другой ячейки <tex>V(s', \Sigma)</tex>. Проверём прямую, которая соответствует кратчайшему расстоянию между <tex>s</tex> и <tex>s'</tex> и рассмотрим точку <tex>p</tex>, которая лежит на её продолжении за <tex>s'</tex> и принадлежит <tex>V(s, \Sigma)</tex>. Такая точка будет существовать, т.к. <tex>V(s', \Sigma)</tex> лежит внутри <tex>V(s, \Sigma)</tex>. Получаем, что кратчайший путь от <tex>p</tex> до <tex>s</tex> проходит через <tex>s'</tex>. Опять противоречие. | ||
| + | }} | ||
{|border="0" width="100%" | {|border="0" width="100%" | ||
Версия 17:59, 16 января 2014
Содержание
Обозначения и определения
Сайт (site) — общее название для точки или замкнутого отрезка .
— внутренняя часть отрезка. Внутренность точки — пустое множество.
Два замкнутых пересекающихся сайта слабо пересекаются (weakly intersect), если точка их пересечения не принадлежит их внутренностям, то есть они касаются концами.
Два сайта сильно пересекаются (strongly intersect), если точка их пересечения принадлежит внутренности хотя бы одного из данных сайтов.
Расстояние от точки до замкнутого сайта : .
Пусть . Ячейка Вороного (Voronoi cell) — множество точек, которые находятся ближе к , чем к любому другому сайту, то есть .
Ребро Вороного (Voronoi edge) — связное множество точек, принадлежащих пересечению ровно двух ячеек Вороного.
Вершина Вороного (Voronoi vertex) — точка, которая принадлежит хотя бы трём ячейкам Вороного.
Диаграмма Вороного (Voronoi diagram) множества сайтов — разбиение плоскости на вершины, рёбра и ячейки Вороного.
1-каркас (1-skeleton) — набор вершин и рёбер Вороного.
В процессе работы алгоритма множество сайтов, которые подаются на вход, может измениться. Чтобы различать начальное и конечное множество сайтов, будем обозначать входное множество через , а множество сайтов, которые присутствуют на результирующей диаграмме Вороного, через . всегда состоит из замкнутых сайтов, а — из точек и открытых отрезков.
Пусть сайты и слабо пересекаются. Тогда битангентная окружность Вороного (bitangent Voronoi circle) — окружность, касающаяся одновременно и . При рассмотрении трёх сайтов , и , окружность, касающаяся всех трёх сайтов, называется тритангентной окружностью Вороного (tritangent Voronoi circle). Точки, принадлежащие рёбрам Вороного, являются центрами битангентных окружностей, а вершины — тритангентных.
Рассмотрим . Будем говорить, что конфликтует с окружностью Вороного , если пересекается с кругом, ограниченным . Также конфликтует с ребром , если он пересекается с кругом, ограниченным одной из окружностей Вороного с центром в точке, принадлежащей . Область конфликтов (conflict region) — множество точек 1-каркаса , соответствующих окружностям Вороного, которые конфликтуют с .
Алгоритм
Рассмотрим сначала алгоритм для слабо пересекающихся сайтов, а потом обобщим его для случая сильно пересекающихся сайтов.
Случай слабо пересекающихся сайтов
Пусть мы уже построили диаграмму Вороного для некоторого множества . Рассмотрим процедуру вставки нового сайта .
Алгоритм состоит из четырёх шагов:
1. Найти первый конфликт сайта с каркасом .
2. Найти всю область конфликтов сайта c каркасом .
3. Построить диаграмму Вороного для .
4. Обновить локализационную структуру.
| Лемма: |
— слабо пересекающееся между собой множество сайтов. Тогда ячейки Вороного — односвязные множества. |
| Доказательство: |
|
Для начала докажем, что ячейки связны. Пусть это не так и у ячейки несколько компонент связности. Рассмотрим — одну из тех, которая не содержит в себе . Начнём идти по кратчайшему пути от любой точки до . Так как и лежат в разных компонентах связности, найдётся , такой что путь проходит через . Значит существует путь от до , который короче, чем , следовательно и . Противоречие. Теперь допустим, что содержит разрыв в виде другой ячейки . Проверём прямую, которая соответствует кратчайшему расстоянию между и и рассмотрим точку , которая лежит на её продолжении за и принадлежит . Такая точка будет существовать, т.к. лежит внутри . Получаем, что кратчайший путь от до проходит через . Опять противоречие. |
|
Таким образом, для нахождения области конфликтов, можно найти одно конфликтующее ребро, а затем, при помощи DFS, найти все остальные.
Пусть сайт — это точка .
Первый шаг алгоритма начинается с поиска ближайшего соседа точки p среди сайтов (если есть несколько ближайших, то подойдёт любой из них). Будем хранить нашу диаграмму в скип-листе для того, чтобы можно было быстро выполнять эти запросы. Либо и — это одна и та же точка, и ничего делать не нужно, либо конфликтует хотя бы с одним ребром, принадлежащим границе ячейки . Тогда первый шаг завершается рассмотрением границы и возвращением одного из рёбер, конфликтующих с . Как было сказано раньше, второй шаг — DFS по рёбрам с целью найти все рёбра, конфликтующие с точкой . После того, как мы узнали , третий шаг будет заключаться в создании новой ячейки Вороного, имеющей границу .
Если же — это замкнутый отрезок , то сначала вставляем конечные точки и , используя процедуру, описанную выше. Остаётся вставить открытый отрезок . Так как и — соседи в диаграмме , обязан конфликтовать с каким-нибудь ребром ячейки, соответствующей или . Таким образом, первый конфликт с можно найти, просматривая рёбра ячейки или , то есть, можно опустить шаг поиска ближайшего соседа. Остаётся найти всю область конфликтов, как и в случае с точкой.
Случай сильно пересекающихся сайтов
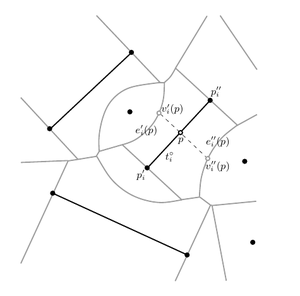
| Пусть — точка, которая сильно пересекается с отрезком , т.е. . Понятно, что будет ближайшим соседом в . Пусть и — два ребра , которые пересекаются с нормалями к , проведёнными из точки (см. рисунок). Пусть и — точки пересечения нормалей с рёбрами и соответственно. Тогда алгоритм вставки точки в диаграмму будет выглядеть следующим образом:
Начинаем с поиска ближайшего соседа . Если , то ничего не делаем. Если — точка, или отрезок, с которым не пересекается, то запускается процедура вставки, которая была описана выше. Иначе — отрезок, пересекающийся с . Сначала добавляем в и заменяем двумя отрезками и , где и — конечные точки . Затем ищем рёбра и , разбиваем их в точках и и добавляем отрезки и в диаграмму. |
Если же мы хотим вставить в диаграмму отрезок , то вставляем сначала его крайние точки и . Затем, начиная с , ищем первый конфликт с текущей диаграммой Вороного и ищем всю область конфликтов. Во время этого поиска, прежде чем тестировать ребро Вороного существующей диаграммы на потенциальный конфликт, мы проверяем, не пересекается ли с одним из сайтов, связанных с . Если такой сайт найден, то поиск останавливается. Если — точка, , то вставляем отрезки и рекурсивно. Если — отрезок , то сначала проверяем, не принадлежит ли один из , другому. Если так и есть, то прекращаем работу, иначе вычисляем точку пересечения отрезков и , вставляем её в диаграмму, а затем рекурсивно вставляем отрезки и .