Алгоритм Фараха

Эта статья находится в разработке!

Алгоритм Фарача — алгоритм построения суффиксного дерева для заданной строки [math]s[/math], ( [math]| s | = N) [/math] который выполняется за время [math]O(N)[/math], при этом даже не требуется выполнения условия конечности алфавита. Такая эффективность достигается за счет того, что строковые последовательности определяются на индексированном алфавите или, что эквивалентно, на целочисленном алфавите [math]\Sigma = \{1, 2 \dots , k\}[/math], при этом накладывается дополнительное условие, что [math]k \in O(N)[/math]. Такие алфавиты часто встречаются на практике.

Описание алгоритма

Основная идея алгоритма, заключается в том что мы уменьшаем размер исходной строки. Для этого мы разбиваем символы сходной строки на пару и пронумеровываем их, а из полученных номеров составляем новую строку, которая уже в [math]2[/math] раза короче.

Алгоритм Фарача будет описан в виде пяти выполняемых шагов. Используем в качестве примера строку [math]s = 121112212221[/math], определенную на алфавите [math]\Sigma = \{1, 2\} [/math] (в этом примере [math]N = 12[/math]).

Шаг 1: суффиксное дерево для сжатой строки

• Строка [math]s[/math] разбивается на пары подряд идущих символов: [math] \lt 12\gt \lt 11\gt \lt 12\gt \lt 21\gt \lt 22\gt \lt 21\gt [/math]

  (если символов нечетное число - последняя пара дополняется специальным символом [math]\$[/math])

• Пары сортируются поразрядной сортировкой: [math]\lt 11\gt \lt 12\gt \lt 12\gt \lt 21\gt \lt 21\gt \lt 22\gt [/math].
• Удаляются копии: [math]\lt 11\gt \lt 12\gt \lt 21\gt \lt 22\gt [/math].
• Парам даются номера (условно, в массиве они и так есть): [math]11-(0), 12-(1), 21-(2), 22-(3)[/math]
• Создаётся новая строка из номеров пар: [math]1 0 1 2 3 2[/math]
• Из полученной строки создаётся суффикcное дерево:

суффиксное дерево для сжатой строки

ID	LCP	STR
1	0	0 1 2 3 2
0	0	1 0 1 2 3 2
2	1	1 2 3 2
3	0	2 3 2
5	1	2
4	0	3 2

Шаг 2: построение четного дерева

Определение:

Четное дерево [math]T^{even}_s[/math] является деревом суффиксов для строки [math]s[/math], узлы-листья которого ограничены нечетными позициями [math]2,4,6, \dots [/math] строки [math]s\$[/math].

Из дерева сжатой строки получаем частичное (чётное) дерево исходной строки. Частичное оно потому, что в нём будет только половина суффиксов, то есть те, которые стоят в чётных позициях:

Очевидно, что для этого достаточно умножить все расстояния в дереве на 2

Корректируются все развилки дерева (так как они могут совпадать в первых символах)

ID	LCP	STR
2	0	1112212221
0	1	121112212221
4	2	12212221
6	0	212221
10	2	21
8	1	2221

Шаг 3: построение нечетного по четному

Определение:

Нечетное дерево [math]T^{odd}_s[/math] является деревом суффиксов для строки [math]s[/math], узлы-листья которого ограничены нечетными позициями [math]1,3,5, \dots [/math] строки [math]s\$[/math].

Из чётного дерева нужно получить нечётное дерево (дерево из суффиксов в нечётных позициях). Для этого можно взять суффиксный массив чётного дерева, отрезать первые символы и выполнить стабильную сортировку по оставшимся первым символам:

нечетное дерево

ID	LCP	STR
3	0	112212221
7	1	12221
11	1	1
1	0	21112212221
5	1	2212221
9	3	221

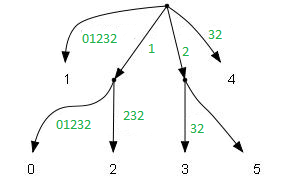
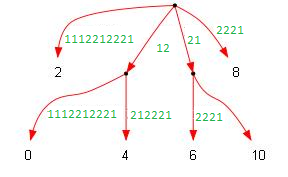
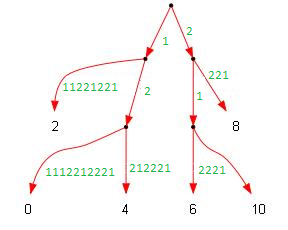
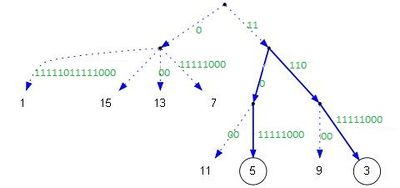
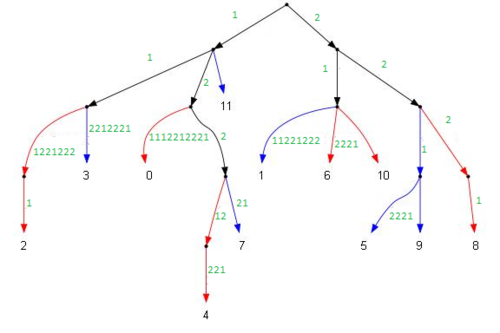
Для выяснения общего префикса строк автор предлагает находить общего предка вершин в суффиксном дереве и считает, что такой предок можно найти за константное время. Для примера в этом дереве, общее начало строк 5 и 9 ([math]11011111000[/math] и [math]1111011111000[/math]) записано в пути от корня до общего предка этих вершин: (рисунок 3-1)

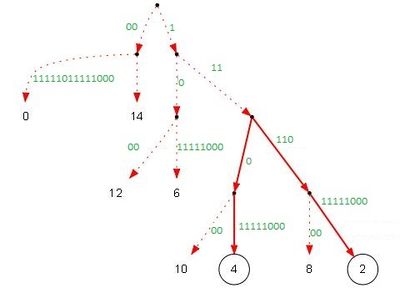
Поскольку структуры нечётного дерева у нас заранее нет и мы её только строим, то подходящих предков мы можем найти в исходном чётном дереве, для этого достаточно проверить вершины с номерами на единицу меньше и отрезать первый символ : (рисунок 3-2).

Шаг 4: слияние четного и нечетного дерева

Далее необходимо найти эффективный способ слияния нечетного и четного деревьев в одно дерево [math]T_s[/math]. Слияние будем производить, начиная с корня. Предположим, что для каждого узла деревьев [math]T_s^{odd}[/math] и [math]T_s^{even}[/math] выходящие из них ребра занесены в специальные списки, где они упорядочены в возрастающем лексикографическом порядке подстрок, которые представляют эти ребра. Алгоритм слияния деревьев просматривает только первые буквы подстрок, представленных ребрами деревьев [math]T_s^{odd}[/math] и [math]T_s^{even}[/math], пусть это будут буквы [math]\lambda^{odd}[/math] и [math]\lambda^{even}[/math]. Тогда:

• если [math]\lambda^{odd}[/math] [math]\ne[/math] [math]\lambda^{even}[/math], определяется поддерево, соответствующее меньшей из этих букв, и без изменений присоединяется к узлу-родителю;
• если [math]\lambda^{odd}[/math] [math]=[/math] [math]\lambda^{even}[/math] и длины подстрок, представленных соответствующими ребрами, равны, в дерево слияния к текущему узлу добавляются два сына: один — из четного дерева, другой — из нечетного;
• если [math]\lambda^{odd}[/math] [math]=[/math] [math]\lambda^{even}[/math] и длины подстрок, представленных соответствующими ребрами, различны, в дерево слияния к текущему узлу добавляются два узла, находящиеся на одном нисходящем пути, при этом ближайший узел будет соответствовать более короткой подстроке.

Если начать эту процедуру для корней нечетного и четного деревьев, далее она рекурсивно выполняется для корней всех поддеревьев, которые, возможно, уже содержат узлы из нечетного и четного деревьев, поскольку ранее мог быть реализован случай [math]\lambda^{odd}[/math] [math]=[/math] [math]\lambda^{even}[/math]. Так как время манипулирования с любым ребром этих деревьев фиксированно, то общее время слияния деревьев составит [math]O(N)[/math].

В результате описанных действий получится дерево [math]M_x[/math], в котором будут присутствовать поддеревья, которые прошли процедуру сличния, и которые ее избежали (то есть были перенесены в дерево [math]M_x[/math] без изменений).

Шаг 5: удаление двойных дуг

Разбираемся с двойными дугами (на этом примере их три). Для этого мы должны выяснить сколько начальных символов таких дуг совпадает. Совпадать может от одного до нескольких символов, или даже все. Проверять их все по очереди нельзя (это даст квадратичное время). Если дуги совпадают полностью, тогда ничего не делаем, удаляем одну из копий и всё. Если начало для двух дуг совпадает только частично, тогда нужно делать для них общее начало, а ветки которые на концах снова развести по разным деревъям (для этого можно во время снияния запомнить их начальный цвет или просто сохранить ссылки на исходные ветки).

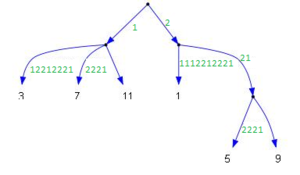
Для примера как это сделать возмём строку [math]10010010101000[/math]:

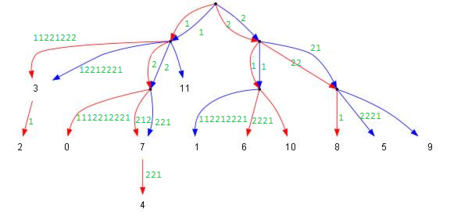
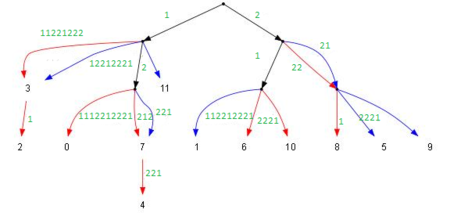
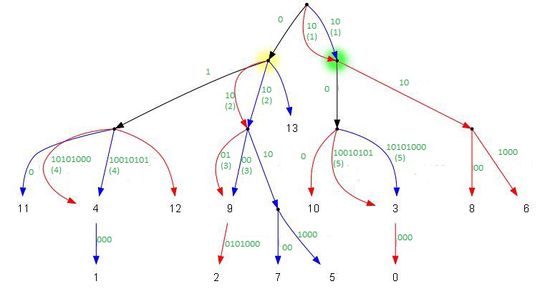
Для того чтобы узнать общее начало двойной дуги, нужно взять одну чётную и одну нечётную на дереве, для которых родителем является конец нашей двойной дуги. Например на рисунке выше двойная дуга [math](1)[/math], конец помечен зелёным - является общим родителем для вершин [math]3[/math] и [math]6[/math]. Чтобы узнать на каком расстоянии будет расслаиваться двойная дуга, надо увеличить номера вершин на еденицу и найти их родителя. Он будет находится на единицу ближе к корню (и путь у вершин будет одинаковой строкой, не считая размера). Родитель вершин [math]4[/math] и [math]7[/math] помечен жёлтым, он находится на расстоянии [math]1[/math] от корня, следовательно дуга [math](1)[/math] должна расслаиваться в двух символах от корня, то есть обе дуги совпадают и их просто надо слить.

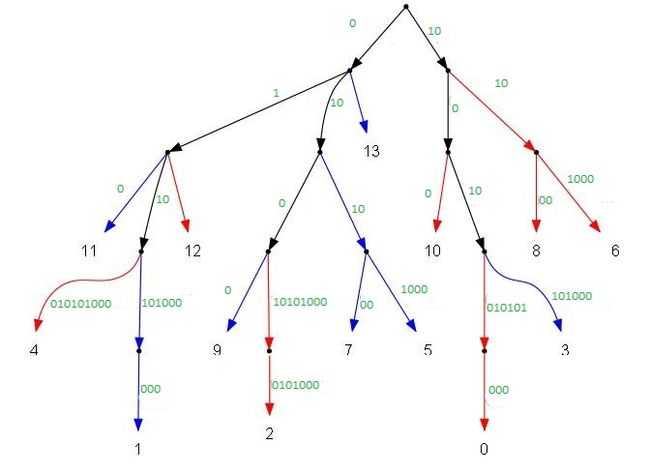
Разберём дуги по порядку:

• [math](1)[/math] расслоение находится на расстоянии два от корня, то есть дуга не расслаивается.
• [math](2)[/math] конец является родителем вершин [math]2[/math], [math]7[/math]. Родитель [math]3[/math], [math]8[/math] после слияния дуги [math](1)[/math], находится на глубине [math]2[/math] символа. Значит дуга [math](2)[/math] расслаивается на глубине [math]3[/math] символа, то есть так же не расслаивается. Дугу [math](2)[/math] нужно вычислять после обработки дуги [math](1)[/math], потому что конец дуги [math](1)[/math] после обработки может оказаться на разной высоте, в зависимости от того на каком символе она расслоилась.
• [math](3)[/math] конец является родителем [math]2[/math], [math]9[/math]. Родитель [math]3[/math], [math]10[/math] находится на расстоянии [math]3[/math], а наше расслоение на на расстоянии [math]4[/math], то есть сливается первый символ двойной дуги. Дугу [math](3)[/math] надо вычислять после дуги [math](2)[/math]. Потому что если на дуге [math](2)[/math] появится разветвление, то компоненты дуги [math](3)[/math] придётся растащить по разным веткам дерева и сравнивать их будет не нужно.
• [math](4)[/math] конец является родителем [math]1[/math], [math]4[/math]. Расслаивается на втором символе.
• [math](5)[/math] конец является родителем [math]0[/math], [math]3[/math]. Дугу [math](5)[/math] можно обрабатывать только после дуги [math](4)[/math], так как от неё будет зависеть глубина расслояния.

Дерево после обработки:

Ссылки

• Суффиксное дерево - Алгоритм фарача
• Optimal suffix tree construction with large alphabets
• Computing Patterns in Strings
• Chris Parjaszewski's implementation

См. также

• Сжатое суффиксное дерево
• Алгоритм Укконена
• Суффиксный массив