Алгоритм Тарьяна поиска LCA за О(1) в оффлайне — различия между версиями
Алесандр (обсуждение | вклад) |
|||
| Строка 7: | Строка 7: | ||
Зафиксируем момент, мы собираемся выйти из вершины <tex>v</tex> (обработали всех сыновей) и хотим узнать ответ для пары <tex>v</tex>, <tex>u</tex>. | Зафиксируем момент, мы собираемся выйти из вершины <tex>v</tex> (обработали всех сыновей) и хотим узнать ответ для пары <tex>v</tex>, <tex>u</tex>. | ||
| − | Тогда заметим что ответ - это либо вершина <tex>v</tex>, либо какой-то её предок. Значит нам нужно найти предок вершины <tex>v</tex>, который является предком вершины <tex>u</tex> с наибольшей глубиной. Заметим, что при фиксированном <tex>v</tex> каждый из предков вершины <tex>v</tex> порождает некоторый класс вершин <tex>u</tex>, для которых он является ответом (в этом классе содержатся все вершины которые находятся "слева" от этого предка). | + | Тогда заметим что ответ {{---}}, это либо вершина <tex>v</tex>, либо какой-то её предок. Значит нам нужно найти предок вершины <tex>v</tex>, который является предком вершины <tex>u</tex> с наибольшей глубиной. Заметим, что при фиксированном <tex>v</tex> каждый из предков вершины <tex>v</tex> порождает некоторый класс вершин <tex>u</tex>, для которых он является ответом (в этом классе содержатся все вершины которые находятся "слева" от этого предка). |
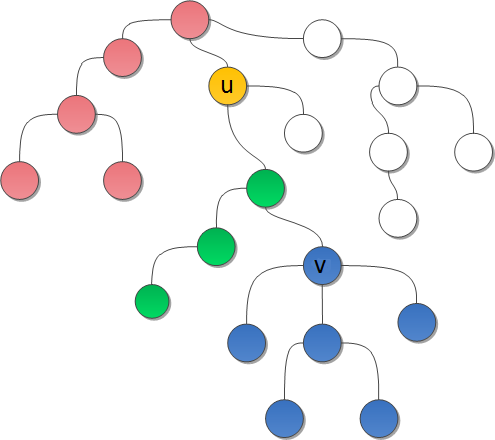
На рисунке разные цвета-разные классы,а белые вершины ещё не просмотренные в <tex>dfs</tex>. | На рисунке разные цвета-разные классы,а белые вершины ещё не просмотренные в <tex>dfs</tex>. | ||
Версия 16:18, 6 июня 2014
Алгоритм Тарьяна позволяет находить наименьшего общего предка двух вершин в дереве, если все запросы известны заранее (offline). Каждый запрос к дереву - это 2 вершины , для которых нужно найти такую вершину , что -предок вершин и , и имеет максимальную глубину из всех таких вершин. Алгоритм позволяет найти ответы для дерева из n вершин и m запросов за время , т.е при достаточно большом m, за на запрос.
Алгоритм
Подвесим наше дерево за любую вершину, и запустим обход в глубину из её. Ответ на каждый запрос мы найдём в течении этого . Ответ для вершин , находится, когда мы уже посетили вершины , а в обработали всех сыновей и собираемся выйти из неё.
Зафиксируем момент, мы собираемся выйти из вершины (обработали всех сыновей) и хотим узнать ответ для пары , . Тогда заметим что ответ —, это либо вершина , либо какой-то её предок. Значит нам нужно найти предок вершины , который является предком вершины с наибольшей глубиной. Заметим, что при фиксированном каждый из предков вершины порождает некоторый класс вершин , для которых он является ответом (в этом классе содержатся все вершины которые находятся "слева" от этого предка).
На рисунке разные цвета-разные классы,а белые вершины ещё не просмотренные в .
Классы этих вершин - не пересекаются, а значит мы их можем эффективно обрабатывать с помощью . Будем поддерживать массив - представитель множества в котором содержится вершина . Для каждого класса мы образуем множество, и представителя этого множества. Когда мы приходим в новую вершину мы должны добавить её в новый класс (), а когда просмотрим всё поддерево какого-то ребёнка, мы должны объединить это поддерево с нашим классом (операция ), и не забыть установить представителя как вершину (в зависимости от реализации это может быть какая-то другая вершина).
Зафиксируем вершины , и выделим путь от корня до этой вершины. Теперь все рёбра "левее" этого пути уже добавлены в , все рёбра правее — ещё не обработаны, а все рёбра на пути — обработаны, но в ещё не добавлены, так как в мы добавляем при выходе. Тогда можно заметить, что любая вершина из обработанных в цепляются к какой-то вершине текущего пути, в . К самой первой вершине этого пути, до которой мы доберёмся, если будем просто подниматься. Очевидно, это и есть .
После того как мы обработали всех детей вершины , мы можем ответить на все запросы вида (,) где -уже посещённая вершина. Нетрудно заметить что ответ для .Так же можно понять что для каждого запроса это условие(что одна вершина уже посещена, а другую мы обрабатываем) выполнится только один раз.
Реализация
vector <bool> visited;
vector <int> query[n];
int dsu_get (int v) {
return v == dsu[v] ? v : dsu[v] = dsu_get (dsu[v]);
}
unite (int a, int b, int new_ancestor) {
a = dsu_get (a);
b = dsu_get (b);
dsu[a] = b;
ancestor[b] = new_ancestor;
}
dfs(int v) {
visited[v] = true;
for (u таких, что (v, u) — ребро в G)
if (not visited[u])
dfs(u);
union(v, u, v);
for (i = 0; i < query[v].size; i++)
if (visited[query[v][i]])
cout << "LCA " << v << " " << u << " = " << ancestor[dsu_get(q[v][i])];
}
int main() {
dfs(1); // можно запускать от любой вершины
}
Оценка сложности
Она состоит из нескольких оценок. Во-первых работает О (n). Во-вторых, операции по объединению множеств, которые в сумме для всех разумных затрачивают операций. В-третьих, для каждого запроса проверка условия и определение результата, опять же, для всех разумных выполняется за . Итоговая асимптотика получается , но при достаточно больших ответ за на один запрос.