Алгоритм Тарьяна поиска LCA за O(1) в оффлайн — различия между версиями
Shersh (обсуждение | вклад) (→Алгоритм) |
Shersh (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | Дано дерево и набор запросов: пары вершин <tex>\langle v, u \rangle </tex>, и для каждой пары нужно найти наименьшего общего предка. Считаем, что все запросы известны заранее, поэтому будем решать задачу оффлайн. | + | Дано дерево <tex> G </tex> и набор запросов: пары вершин <tex>\langle v, u \rangle </tex>, и для каждой пары нужно найти наименьшего общего предка. Считаем, что все запросы известны заранее, поэтому будем решать задачу оффлайн. |
Алгоритм позволяет найти ответы для дерева из <tex>n</tex> вершин и <tex>m</tex> запросов за время <tex>O (n + m)</tex>, то есть при достаточно большом <tex>m</tex> за <tex>O (1)</tex> на запрос. | Алгоритм позволяет найти ответы для дерева из <tex>n</tex> вершин и <tex>m</tex> запросов за время <tex>O (n + m)</tex>, то есть при достаточно большом <tex>m</tex> за <tex>O (1)</tex> на запрос. | ||
== Алгоритм == | == Алгоритм == | ||
| Строка 6: | Строка 6: | ||
Зафиксируем момент: мы собираемся выйти из вершины <tex>v</tex> (обработали всех сыновей) и хотим узнать ответ для пары <tex>\langle v</tex>, <tex>u \rangle</tex>. | Зафиксируем момент: мы собираемся выйти из вершины <tex>v</tex> (обработали всех сыновей) и хотим узнать ответ для пары <tex>\langle v</tex>, <tex>u \rangle</tex>. | ||
| − | Тогда заметим, что ответ {{---}} это либо вершина <tex>u</tex>, либо какой-то её предок. Значит, нам нужно найти предка вершины <tex>v</tex>, который является предком вершины <tex>u</tex> с наибольшей глубиной. Заметим, что при фиксированном <tex>v</tex> каждый из предков вершины <tex>v</tex> порождает некоторый класс вершин <tex>u</tex>, для которых он является ответом, в этом классе содержатся все вершины которые находятся "слева" от этого предка. | + | Тогда заметим, что ответ {{---}} это либо вершина <tex>u</tex>, либо какой-то её предок. Значит, нам нужно найти предка вершины <tex>v</tex>, который является предком вершины <tex>u</tex> с наибольшей глубиной. Заметим, что при фиксированном <tex>v</tex> каждый из предков вершины <tex>v</tex> порождает некоторый класс вершин <tex>u</tex>, для которых он является ответом, в этом классе содержатся все вершины, которые находятся "слева" от этого предка. |
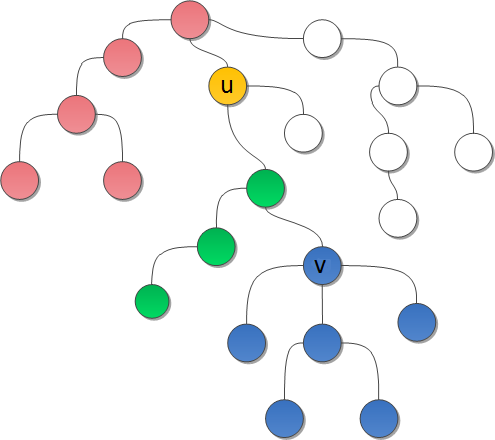
На рисунке разные цвета {{---}} разные классы, а белые вершины {{---}} ещё не просмотренные в <tex>dfs</tex>. | На рисунке разные цвета {{---}} разные классы, а белые вершины {{---}} ещё не просмотренные в <tex>dfs</tex>. | ||
| Строка 17: | Строка 17: | ||
Обновление массива <tex> ancestor </tex> будем производить следующим образом: | Обновление массива <tex> ancestor </tex> будем производить следующим образом: | ||
| − | * когда мы приходим в новую вершину <tex>v</tex> мы должны добавить её в новый класс {{---}} <tex>ancestor[v] = v</tex> | + | * когда мы приходим в новую вершину <tex>v</tex>, мы должны добавить её в новый класс {{---}} <tex>ancestor[v] = v</tex> |
* когда просмотрим всё поддерево какого-то ребёнка <tex> u </tex> у вершины <tex> v </tex>, мы должны объединить поддерево ребёнка с классом вершины <tex> v </tex> (<tex>\mathrm{union}(v, u, v)</tex> {{---}} объединить классы вершин <tex> v </tex> и <tex> u </tex>, а наименьшим общим предком представителя нового класса сделать вершину <tex> v </tex>). Система непересекающихся множеств сама определит представителя в зависимости от используемой нами эвристики. Нам надо лишь правильно установить значение массива <tex> ancestor </tex> у нового представителя. | * когда просмотрим всё поддерево какого-то ребёнка <tex> u </tex> у вершины <tex> v </tex>, мы должны объединить поддерево ребёнка с классом вершины <tex> v </tex> (<tex>\mathrm{union}(v, u, v)</tex> {{---}} объединить классы вершин <tex> v </tex> и <tex> u </tex>, а наименьшим общим предком представителя нового класса сделать вершину <tex> v </tex>). Система непересекающихся множеств сама определит представителя в зависимости от используемой нами эвристики. Нам надо лишь правильно установить значение массива <tex> ancestor </tex> у нового представителя. | ||
| Строка 49: | Строка 49: | ||
Пусть теперь наименьшим общим предком вершин <tex> u </tex> и <tex> v </tex> будет вершина, отличная от этих двух. Во время обработки запроса алгоритм точно вернёт общего предка этих двух вершин, так как он будет предком одной из вершин по массиву <tex> ancestor </tex>, а предком другой из-за обхода в глубину. | Пусть теперь наименьшим общим предком вершин <tex> u </tex> и <tex> v </tex> будет вершина, отличная от этих двух. Во время обработки запроса алгоритм точно вернёт общего предка этих двух вершин, так как он будет предком одной из вершин по массиву <tex> ancestor </tex>, а предком другой из-за обхода в глубину. | ||
| − | Покажем, что найдём наименьшего предка. Пусть это не так. Тогда существует какая-то вершина <tex> w </tex>, которая тоже является предком вершин <tex> u </tex> и <tex> v </tex> и из которой мы вышли раньше во время обхода в глубину. Но тогда ситуация, что одна из вершин посещена, а у другой рассмотрены все дети, должна была выполниться раньше, и в качестве ответа должна была вернуться вершина <tex> w </tex>. | + | Покажем, что найдём наименьшего предка. Пусть это не так. Тогда существует какая-то вершина <tex> w </tex>, которая тоже является предком вершин <tex> u </tex> и <tex> v </tex>, и из которой мы вышли раньше во время обхода в глубину. Но тогда ситуация, что одна из вершин посещена, а у другой рассмотрены все дети, должна была выполниться раньше, и в качестве ответа должна была вернуться вершина <tex> w </tex>. |
Заметим, что для корректности алгоритма достаточно было бы одного массива <tex> dsu </tex>, а представителем класса всегда выбирать наименьшего общего предка вершин класса. Это несложно сделать, так как мы всегда объединяем ребёнка со своим родителем. Но в таком случае алгорим получился бы менее эффективным, потому что одна только эвристика сжатия путей работает недостаточно быстро. | Заметим, что для корректности алгоритма достаточно было бы одного массива <tex> dsu </tex>, а представителем класса всегда выбирать наименьшего общего предка вершин класса. Это несложно сделать, так как мы всегда объединяем ребёнка со своим родителем. Но в таком случае алгорим получился бы менее эффективным, потому что одна только эвристика сжатия путей работает недостаточно быстро. | ||
| Строка 56: | Строка 56: | ||
Она состоит из нескольких оценок. | Она состоит из нескольких оценок. | ||
| − | *Обход в глубину | + | *Обход в глубину выполняется за <tex>O(n)</tex>. |
| − | *Операции по объединению множеств, которые в сумме для всех разумных <tex>n</tex> | + | *Операции по объединению множеств, которые в сумме для всех разумных <tex>n</tex> работают <tex>O (n)</tex> времени. Каждый запрос <tex>\langle v, u \rangle </tex> будет рассмотрен дважды {{---}} при посещении вершины <tex>u</tex> и <tex>v</tex>, но обработан лишь один раз, поэтому можно считать, что все запросы обработаются суммарно за <tex>O (m)</tex>. |
*Для каждого запроса проверка условия и определение результата, опять же, для всех разумных <tex>n</tex> выполняется за <tex>O (1)</tex>. | *Для каждого запроса проверка условия и определение результата, опять же, для всех разумных <tex>n</tex> выполняется за <tex>O (1)</tex>. | ||
| − | + | Следовательно, итоговая асимптотика составляет <tex>O (n + m)</tex>, но при достаточно больших <tex>m</tex> ответ за <tex>O (1)</tex> на один запрос. | |
== Источники информации == | == Источники информации == | ||
Версия 20:23, 9 июня 2014
Дано дерево и набор запросов: пары вершин , и для каждой пары нужно найти наименьшего общего предка. Считаем, что все запросы известны заранее, поэтому будем решать задачу оффлайн. Алгоритм позволяет найти ответы для дерева из вершин и запросов за время , то есть при достаточно большом за на запрос.
Алгоритм
Подвесим наше дерево за любую вершину, и запустим обход в глубину из неё. Ответ на каждый запрос мы найдём в течение поиска в глубину. Ответ для вершин и находится, когда мы уже посетили вершину , а также посетили всех сыновей вершины и собираемся выйти из неё.
Зафиксируем момент: мы собираемся выйти из вершины (обработали всех сыновей) и хотим узнать ответ для пары , . Тогда заметим, что ответ — это либо вершина , либо какой-то её предок. Значит, нам нужно найти предка вершины , который является предком вершины с наибольшей глубиной. Заметим, что при фиксированном каждый из предков вершины порождает некоторый класс вершин , для которых он является ответом, в этом классе содержатся все вершины, которые находятся "слева" от этого предка.
На рисунке разные цвета — разные классы, а белые вершины — ещё не просмотренные в .
Классы этих вершин не пересекаются, а значит, мы можем их эффективно обрабатывать с помощью системы непересекающихся множеств, которую будем хранить в массиве .
Будем поддерживать также массив , где — наименьший общий предок всех вершин, которые лежат в том же классе, что и . Обновление массива для каждого элемента будет неэффективно. Поэтому зафиксируем в каждом классе какого-то представителя. Функция вернёт представителя класса, в котором находится вершина . Тогда наименьшим общим предком всех вершин из класса будет вершина .
Обновление массива будем производить следующим образом:
- когда мы приходим в новую вершину , мы должны добавить её в новый класс —
- когда просмотрим всё поддерево какого-то ребёнка у вершины , мы должны объединить поддерево ребёнка с классом вершины ( — объединить классы вершин и , а наименьшим общим предком представителя нового класса сделать вершину ). Система непересекающихся множеств сама определит представителя в зависимости от используемой нами эвристики. Нам надо лишь правильно установить значение массива у нового представителя.
После того как мы обработали всех детей вершины , мы можем ответить на все запросы вида , где — уже посещённая вершина. Нетрудно заметить, что . Для каждого запроса это условие (что одна вершина уже посещена, а другую мы обрабатываем) выполнится только один раз.
Реализация
bool visited[n]
function union(x : int, y : int, newAncestor : int):
leader = dsuUnion(x, y) // объединяем классы вершин и и получаем нового представителя класса
ancestor[leader] = newAncestor // устанавливаем нового предка представителю множества
// можно запустить от любой вершины дерева в самый первый раз
function dfs(v : int):
visited[v] = true
ancestor[v] = v
foreach u : (v, u) in G
if not visited[u]
dfs(u)
union(v, u, v)
foreach u : — есть такой запрос
if visited[u]
запомнить, что ответ для запроса = ancestor[find[u]]
Корректность
Случай, когда является наименьшим общим предком вершин и , обработается правильно, потому что по алгоритму в этот момент .
Пусть теперь наименьшим общим предком вершин и будет вершина, отличная от этих двух. Во время обработки запроса алгоритм точно вернёт общего предка этих двух вершин, так как он будет предком одной из вершин по массиву , а предком другой из-за обхода в глубину.
Покажем, что найдём наименьшего предка. Пусть это не так. Тогда существует какая-то вершина , которая тоже является предком вершин и , и из которой мы вышли раньше во время обхода в глубину. Но тогда ситуация, что одна из вершин посещена, а у другой рассмотрены все дети, должна была выполниться раньше, и в качестве ответа должна была вернуться вершина .
Заметим, что для корректности алгоритма достаточно было бы одного массива , а представителем класса всегда выбирать наименьшего общего предка вершин класса. Это несложно сделать, так как мы всегда объединяем ребёнка со своим родителем. Но в таком случае алгорим получился бы менее эффективным, потому что одна только эвристика сжатия путей работает недостаточно быстро.
Оценка сложности
Она состоит из нескольких оценок.
- Обход в глубину выполняется за .
- Операции по объединению множеств, которые в сумме для всех разумных работают времени. Каждый запрос будет рассмотрен дважды — при посещении вершины и , но обработан лишь один раз, поэтому можно считать, что все запросы обработаются суммарно за .
- Для каждого запроса проверка условия и определение результата, опять же, для всех разумных выполняется за .
Следовательно, итоговая асимптотика составляет , но при достаточно больших ответ за на один запрос.