Алгоритм Касаи и др.

Алгоритм Касаи (Аримуры-Арикавы-Касаи-Ли-Парка) — алгоритм, позволяющий за линейное время вычислить длину наибольших общих префиксов для соседних циклических сдвигов строки, отсортированных в лексикографическом порядке (largest common prefix, далее [math]LCP[/math]).

Обозначения

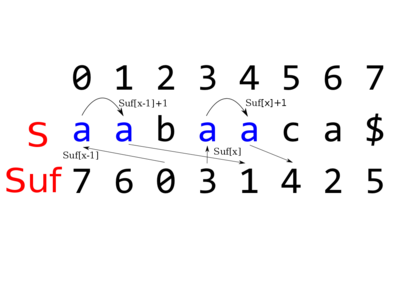
Задана строка [math]S[/math]. Тогда [math]S_{i}[/math] — суффикс строки [math]S[/math], начинающийся в [math]i[/math]-ом символе. Пусть задан суффиксный массив [math]Suf[/math]. Для вычисления [math]LCP[/math] будем использовать промежуточный массив [math]Suf^{-1}[/math]. Массив [math]Suf^{-1}[/math] определен как обратный к массиву [math]Suf[/math]. Он может быть получен немедленно, если задан массив [math]Suf[/math]. Если [math]Suf[k] = i[/math], то [math]Suf^{-1}[i] = k[/math].

[math]Height[i][/math] — длина наибольшего общего префикса [math]i[/math] и [math]i-1[/math] строк в суффиксном массиве ([math]Suf[i][/math] и [math]Suf[i-1][/math] соответственно).

Некоторые свойства [math]LCP[/math]

Факт №1

[math]LCP[/math] между двумя суффиксами — это минимум [math]LCP[/math] всех пар соседних суффиксов между ними в суффиксном массиве [math]Suf[/math]. То есть [math]LCP(S_{Suf[x]}, S_{Suf[z]}) = \min_{x \lt y \leqslant z}(LCP(S_{Suf[y - 1]},S_{Suf[y]})[/math]. Отсюда следует, что [math]LCP[/math] пары соседних суффиксов в массиве [math]Suf[/math] больше или равно [math]LCP[/math] пары суффиксов, окружающих их.

Утверждение:

[math]LCP(S_{Suf[y - 1]}, S_{Suf[y]}) \geqslant LCP(S_{Suf[x]},S_{Suf[z]}), x \lt y \leqslant z[/math]

Факт №2

Если значение [math]LCP[/math] между парой суффиксов, соседних в массиве [math]Suf[/math], больше [math]1[/math], то можно удалить первый символ каждого суффикса и лексикографический порядок суффиксов сохранится.

Утверждение:

Если [math]LCP(S_{Suf[x-1]} , S_{Suf[x]} ) \gt 1[/math], тогда [math]Suf^{-1}[Suf[x - 1] + 1] \lt Suf^{-1}[Suf[x] + 1][/math]

Пояснительная картинка к факту 2 и 3

Факт №3

В этом же случае, значение [math]LCP[/math] между [math]S_{Suf[x-1]+1}[/math] и [math]S_{Suf[x]+1}[/math] на один меньше значения [math]LCP[/math] между [math]S_{Suf[x-1]}[/math] и [math]S_{Suf[x]}[/math].

Утверждение:

Если [math]LCP(S_{Suf[x-1]} , S_{Suf[x]} ) \gt 1[/math], тогда [math]LCP(S_{Suf[x-1]+1} , S_{Suf[x]+1}) = LCP(S_{Suf[x-1]} , S_{Suf[x]} ) - 1[/math]

Вспомогательные утверждения

Теперь рассмотрим следующую задачу: рассчитать [math]LCP[/math] между суффиксом [math]S_{i}[/math] и его соседним суффиксом в массиве [math]Suf[/math], при условии, что значение [math]LCP[/math] между [math]S_{i-1}[/math] и его соседним суффиксом известны. Для удобства записи пусть [math]p=Suf^{-1}[i - 1][/math] и [math]q = Suf^{-1}[i][/math]. Так же пусть [math]j - 1 = Suf[p-1][/math] и [math]k = Suf[q - 1][/math]. Проще говоря, мы хотим посчитать [math]Height[q][/math], когда задано [math]Height[p][/math]

Лемма:

Если [math]LCP(S_{j-1}, S_{i-1}) \gt 1[/math], тогда [math]LCP(S_k,S_i) \geqslant LCP(S_j,S_i)[/math]

Доказательство:

[math]\triangleright[/math]

Так как [math]LCP(S_{j-1},S_{i-1}) \gt 1[/math], имеем [math]Suf^{-1}[j] \lt Suf^{-1}[i][/math] из факта №2. Так как [math]Suf^{-1}[j] \leqslant Suf^{-1}[k] = Suf^{-1}[i] - 1[/math], имеем [math]LCP(S_{k} , S_{i}) \geqslant LCP(S_{j} , S_{i})[/math] из факта №1

[math]\triangleleft[/math]

Теорема:

Если [math]Height[p] = LCP(S_{j-1}, S_{i-1}) \gt 1[/math], то [math]Height[q] = LCP(S_{k}, S_{i}) \geqslant Height[p] - 1[/math]

Доказательство:

[math]\triangleright[/math]

[math]LCP(S_{k}, S_{i}) \geqslant LCP(S_{j} , S_{i})[/math] (из леммы) [math]LCP(S_{j} , S_{i}) = LCP(S_{j-1}, S_{i-1}) - 1[/math] (из факта №3). Значит, [math]LCP(S_{k}, S_{i}) \geqslant LCP(S_{j-1}, S_{i-1}) - 1[/math]

[math]\triangleleft[/math]

Описание алгоритма и псевдокод

Таким образом, начиная проверять [math]LCP[/math] для текущего суффикса не с первого символа, а с указанного, можно за линейное время построить [math]LCP[/math]. Покажем, что построение [math]LCP[/math] таким образом действительно требует [math]O(N)[/math] времени. Действительно, на каждой итерации текущее значение [math]LCP[/math] может быть не более чем на единицу меньше предыдущего. Таким образом, значения [math]LCP[/math] в сумме могут увеличиться не более, чем на [math]2N[/math] (с точностью до константы). Следовательно, алгоритм построит [math]LCP[/math] за [math]O(N)[/math].

int[] build_lcp(str : string, suf : int[])  // str — исходная строка с добавленным специальным символом $ 
                                            // suf[] — суффиксный массив строки str  
   int len [math]\leftarrow[/math] str.length
   int[len] lcp
   int[len] pos                             // pos[] — массив, обратный массиву suf 
   for i = 0 to len - 1
      pos[suf[i]] [math]\leftarrow[/math] i
   int k [math]\leftarrow[/math] 0
   for i = 0 to len - 1
      if k > 0
         k--  
      if pos[i] == len - 1
         lcp[len - 1] [math]\leftarrow[/math] -1
         k [math]\leftarrow[/math] 0
      else
         int j [math]\leftarrow[/math] suf[pos[i] + 1]
         while str[i + k] == str[j + k]
            k++
         lcp[pos[i]] [math]\leftarrow[/math] k;
   return lcp

Источники информации

• Википедия — Алгоритм Касаи
• T.Kasai, G.Lee, H.Arimura, S.Arikawa, K.Park - Linear-Time Longest-Common-Prefix Computation in Suffix Arrays and Its Application