Матрица смежности графа — различия между версиями
(Добавлены категории) |
(вставка шаблона) |
||
| Строка 1: | Строка 1: | ||
| − | + | __NOTOC__ | |
| − | '''Матрицей смежности''' (англ. Adjacency matrix) <tex>A=||\alpha_{i,j}||</tex> ''помеченного графа'' <tex>G(V,E)</tex> называется матрица <tex>A_{[V\times{}V]}</tex>, в которой <tex>\alpha_{i,j}</tex> — количество рёбер, соединяющих вершины <tex>v_i</tex> и <tex>v_j</tex>, причём при <tex>i=j</tex> каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. | + | {{Определение |
| + | |definition ='''Матрицей смежности''' (англ. Adjacency matrix) <tex>A=||\alpha_{i,j}||</tex> ''помеченного графа'' <tex>G(V,E)</tex> называется матрица <tex>A_{[V\times{}V]}</tex>, в которой <tex>\alpha_{i,j}</tex> — количество рёбер, соединяющих вершины <tex>v_i</tex> и <tex>v_j</tex>, причём при <tex>i=j</tex> каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. | ||
| + | }} | ||
| − | + | == Пример == | |
{| border="1" cellpadding="5" cellspacing="0" style="text-align:center" | {| border="1" cellpadding="5" cellspacing="0" style="text-align:center" | ||
!style="background:#f2f2f2"|Граф | !style="background:#f2f2f2"|Граф | ||
| Строка 20: | Строка 22: | ||
Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц), причём её главная диагональ целиком состоит из нулей. | Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц), причём её главная диагональ целиком состоит из нулей. | ||
| − | === | + | === Случай ориентированного графа === |
| − | Сумма элементов <tex>i</tex>-й строки равна <tex>\deg^- v_i</tex>, то есть < | + | Сумма элементов <tex>i</tex>-й строки равна <tex>\deg^- v_i</tex>, то есть <tex>\sum\limits_{j=1}^{n}\alpha_{i,j} = \deg^- v_i</tex>. |
| − | Аналогично сумма элементов <tex>j</tex>-го стоблца равна <tex>\deg^+ v_j</tex>, то есть < | + | Аналогично сумма элементов <tex>j</tex>-го стоблца равна <tex>\deg^+ v_j</tex>, то есть <tex>\sum\limits_{i=1}^{n}\alpha_{i,j} = \deg^+ v_j</tex>. |
| − | === | + | === Случай неориентированного графа === |
Для неориентированных графов матрица смежности является симметричной. | Для неориентированных графов матрица смежности является симметричной. | ||
| − | Сумма элементов <tex>i</tex>-й строки равна <tex>\deg v_i</tex>, то есть < | + | Сумма элементов <tex>i</tex>-й строки равна <tex>\deg v_i</tex>, то есть <tex>\sum\limits_{j=1}^{n}\alpha_{i,j} = \deg v_i</tex>. В следствии симметричности суммы элементов <tex>i</tex>-й строки и <tex>i</tex>-го столбца равны. |
== См. также == | == См. также == | ||
Версия 00:17, 14 октября 2010
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) помеченного графа называется матрица , в которой — количество рёбер, соединяющих вершины и , причём при каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. |
Пример
| Граф | Матрица смежности |
|---|---|
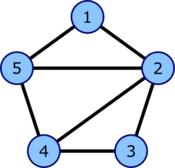
|
Свойства
Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц), причём её главная диагональ целиком состоит из нулей.
Случай ориентированного графа
Сумма элементов -й строки равна , то есть . Аналогично сумма элементов -го стоблца равна , то есть .
Случай неориентированного графа
Для неориентированных графов матрица смежности является симметричной.
Сумма элементов -й строки равна , то есть . В следствии симметричности суммы элементов -й строки и -го столбца равны.
См. также
Литература
- Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5