Алгоритм Ландау-Вишкина (k несовпадений) — различия между версиями
Margarita (обсуждение | вклад) (→Пример) |
Margarita (обсуждение | вклад) (→Алгоритм) |
||
| Строка 3: | Строка 3: | ||
==Алгоритм== | ==Алгоритм== | ||
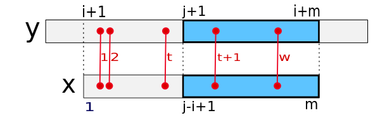
| + | [[Файл:algLandauVishkin1.png|thumb|380px|right| В таблицу tm по номеру несовпадения записывается соответстующий индекс образца.]] | ||
| + | |||
При анализе текста используется двумерный массив <tex>tm[0...n-m][1...k+1]</tex>, содержащий информацию о несовпадениях текста с образцом. По завершении анализа в его <tex>i</tex>-й строке содержатся позиции в <tex>x</tex> первых <tex>k+1</tex> несовпадений между строками <tex>x[1...m]</tex> и <tex>y[i+1...i+m]</tex>. Таким образом, если <tex>tm[i][v] = s</tex>, то <tex>y[i+s] \neq x[s]</tex>, и это <tex>v</tex>-е несовпадение между <tex>x[1...m]</tex> и <tex>y[i+1...i+m]</tex>, считая слева направо. Если число <tex>d</tex> несовпадений <tex>x[1...m]</tex> с подстрокой <tex>y[i+1...i+m]</tex> меньше <tex>k+1</tex>, то, начиная с <tex>d+1</tex>, элементы <tex>i</tex>-й строки равны значению по умолчанию <tex>m+1</tex>. | При анализе текста используется двумерный массив <tex>tm[0...n-m][1...k+1]</tex>, содержащий информацию о несовпадениях текста с образцом. По завершении анализа в его <tex>i</tex>-й строке содержатся позиции в <tex>x</tex> первых <tex>k+1</tex> несовпадений между строками <tex>x[1...m]</tex> и <tex>y[i+1...i+m]</tex>. Таким образом, если <tex>tm[i][v] = s</tex>, то <tex>y[i+s] \neq x[s]</tex>, и это <tex>v</tex>-е несовпадение между <tex>x[1...m]</tex> и <tex>y[i+1...i+m]</tex>, считая слева направо. Если число <tex>d</tex> несовпадений <tex>x[1...m]</tex> с подстрокой <tex>y[i+1...i+m]</tex> меньше <tex>k+1</tex>, то, начиная с <tex>d+1</tex>, элементы <tex>i</tex>-й строки равны значению по умолчанию <tex>m+1</tex>. | ||
| − | |||
| − | |||
Заметим, если <tex>tm[i][k+1] = m+1</tex>, то подстрока <tex>y[i+1...i+m]</tex> отличается от образца <tex>x</tex> не более, чем на <tex>k</tex> символов, и, таким образом, является решением задачи. | Заметим, если <tex>tm[i][k+1] = m+1</tex>, то подстрока <tex>y[i+1...i+m]</tex> отличается от образца <tex>x</tex> не более, чем на <tex>k</tex> символов, и, таким образом, является решением задачи. | ||
| − | + | Затем образец сканируется параллельно с текстом слева на права по одному символу за раз. На итерации <tex>i</tex> с образцом сравнивается подстрока <tex>y[i+1...i+m]</tex>. <tex>j</tex> - обозначим самую правую позицию в тексте, достигнутую за предыдущие итерации, то есть <tex>j</tex> является максимальным из чисел <tex>r+tm[r, k + 1]</tex>, где <tex>0 \leqslant r < i</tex>. Если <tex>i < j</tex>, в <tex>b</tex> присваивается результат работы <tex>merge</tex>, которая находит количество несовпадений между <tex>x[1... j-i]</tex> и <tex>y[i+1...j]</tex>. Если <tex>b</tex> не превышает <tex>k</tex>, вызывается процедура <tex>extend</tex>, которая сравнивает подстроки <tex>y[j + 1...i + m]</tex> и <tex>x[j - i + 1...m]</tex>. | |
| − | |||
| − | Затем образец сканируется параллельно с текстом слева на права по одному символу за раз. На итерации <tex>i</tex> с образцом сравнивается подстрока <tex>y[i+1...i+m]</tex>. <tex>j</tex> - обозначим самую правую позицию в тексте, достигнутую за предыдущие итерации, то есть <tex>j</tex> является максимальным из чисел <tex>r+tm[r, k + 1]</tex>, где <tex>0 | ||
Переменная <tex>r</tex> будет рассмотренна ниже. | Переменная <tex>r</tex> будет рассмотренна ниже. | ||
| Строка 30: | Строка 28: | ||
|} | |} | ||
| − | и в случае несовпадения <tex>b</tex> увеличивается и таблица текстовых несовпадений обновляется. | + | [[Файл:algLandauVishkin2.png|thumb|380px|right| В таблицу tm по номеру несовпадения записывается соответстующий индекс образца.]] |
| + | |||
| + | Рассмотрим процедуру <tex>extend</tex> подробнее. Она сравнивает подстроки <tex>y[j + 1...i + m]</tex> и <tex>x[j - i + 1...m]</tex>, в случае несовпадения <tex>b</tex> увеличивается и таблица текстовых несовпадений обновляется. Это происходит пока либо не будет найдено <tex>k + 1</tex> несовпадений, либо не будет достигнуто <tex>y[i+m]</tex> с не больше чем <tex>k</tex> несовпадениями, то есть найдено вхождение образца, начинающееся с <tex>y[i+1]</tex>. | ||
==Пример== | ==Пример== | ||
Версия 15:50, 15 июня 2014
Постановка задачи
Дано число текст и образец , . Требуется найти все подстроки текста длины , с не более чем несовпадающими символами.
Алгоритм
При анализе текста используется двумерный массив , содержащий информацию о несовпадениях текста с образцом. По завершении анализа в его -й строке содержатся позиции в первых несовпадений между строками и . Таким образом, если , то , и это -е несовпадение между и , считая слева направо. Если число несовпадений с подстрокой меньше , то, начиная с , элементы -й строки равны значению по умолчанию .
Заметим, если , то подстрока отличается от образца не более, чем на символов, и, таким образом, является решением задачи.
Затем образец сканируется параллельно с текстом слева на права по одному символу за раз. На итерации с образцом сравнивается подстрока . - обозначим самую правую позицию в тексте, достигнутую за предыдущие итерации, то есть является максимальным из чисел , где . Если , в присваивается результат работы , которая находит количество несовпадений между и . Если не превышает , вызывается процедура , которая сравнивает подстроки и . Переменная будет рассмотренна ниже.
|
tm[0...n-m][1...k+1] = m+1 // инициализация
r = 0
j = 0
for i = 0 to n - m
b = 0
if i < j
b = merge(i, r, j)
if b < k + 1
r = i
extend(i, j, b)
|
Рассмотрим процедуру подробнее. Она сравнивает подстроки и , в случае несовпадения увеличивается и таблица текстовых несовпадений обновляется. Это происходит пока либо не будет найдено несовпадений, либо не будет достигнуто с не больше чем несовпадениями, то есть найдено вхождение образца, начинающееся с .
Пример
Пусть , , .
| tm | 1 | 2 | 3 | x[1..m] | y[i+1..i+m] |
| 0 | 2 | 3 | 4 | tram | thet |
| 1 | 1 | 2 | 3 | tram | hetr |
| 2 | 1 | 2 | 3 | tram | etri |
| 3 | 3 | 4 | 5 | tram | trip |
| 4 | 1 | 2 | 3 | tram | ripp |
| 5 | 1 | 2 | 3 | tram | ippe |
| 6 | 1 | 2 | 3 | tram | pped |
| 7 | 1 | 2 | 3 | tram | pedt |
| 8 | 1 | 2 | 3 | tram | edtr |
| 9 | 1 | 2 | 3 | tram | dtra |
| 10 | 4 | 5 | 5 | tram | trap |
| tm | 1 | 2 | 3 | 4 | 5 | x[1..m-i] | x[i+1..m] |
| 1 | 1 | 2 | 3 | 5 | 5 | tra | ram |
| 2 | 1 | 2 | 5 | 5 | 5 | tr | am |
| 3 | 1 | 5 | 5 | 5 | 5 | t | m |