Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора

Определение:

Контекстно-свободной грамматикой называется грамматика, у которой в левых частях всех правил стоят только одиночные нетерминалы.

Язык, задаваемый контекстно-свободной грамматикой называется контекстно-свободным языком.

Определение:

Выводом слова [math]\alpha[/math] называется последовательность строк, состоящих из терминалов и нетерминалов, где первой идет строка, состоящая из одного стартового нетерминала, а каждая последующая строка получена из предыдущей путем замены любого нетерминала по одному (любому) из правил, и последней строкой в последовательности является слово [math]\alpha[/math].

Рассмотрим на примере грамматики, выводящей все правильные скобочные последовательности. Терминальные символы "(" и ")", нетерминал [math]S[/math], он же стартовый нетерминал, правила:
[math]S\rightarrow (S)S[/math]
[math]S\rightarrow S(S)[/math]
[math]S\rightarrow \varepsilon[/math]
Выведем слово "(()(()))()":
[math]\boldsymbol{S}\rightarrow (S)\boldsymbol{S} \rightarrow (S)(\boldsymbol{S})S\rightarrow(S)()\boldsymbol{S}\rightarrow(\boldsymbol{S})()\rightarrow(\boldsymbol{S}(S))()\rightarrow(S(S)(\boldsymbol{S}))()\rightarrow(S(S)(\boldsymbol{S}(S)))()\rightarrow (S(\boldsymbol{S})((S)))()\rightarrow(\boldsymbol{S}()((S)))()\rightarrow(()((\boldsymbol{S})))()\rightarrow(()(()))()[/math]

Определение:

Левосторонним выводом слова [math]\alpha[/math] называется его вывод такой, что каждая последующая строка получена из предыдущей путем замены самого левого встречающегося в строке нетерминала по одному из правил.

Аналогичным образом определяется правосторонний вывод.
Рассмотрим левосторонний вывод нашей скобочной последовательности:
[math]\boldsymbol{S}\rightarrow (\boldsymbol{S})S \rightarrow ((\boldsymbol{S})S)S\rightarrow (()\boldsymbol{S})S\rightarrow(()\boldsymbol{S}(S))S\rightarrow(()(\boldsymbol{S}))S\rightarrow(()(\boldsymbol{S}(S)))S\rightarrow(()((\boldsymbol{S})))S\rightarrow(()(()))\boldsymbol{S}\rightarrow(()(()))(\boldsymbol{S})S\rightarrow(()(()))()\boldsymbol{S}\rightarrow(()(()))()[/math]

Определение:

Деревом разбора называется дерево, на вершинах которого записаны терминалы или нетерминалы, а дети вершины, на которой записан нетерминал, соответствуют раскрытию нетерминала по одному любому правилу, в левой части которого стоит этот нетерминал, и упорядочены так же, как в правой части этого правила. Все вершины, помеченные терминалами, являются листьями. Все вершины, помеченные нетерминалами имеют детей.

Определение:

Кроной дерева разбора называется множество терминальных символов, упорядоченное в соответствии с номерами их достижения при обходе дерева из в глубину корня.

Крона дерева разбора представляет из себя слово языка, которое выводит это дерево.
Рассмотрим, как будет выглядеть дерево разбора нашей скобочной последовательности.
[[Файл:]]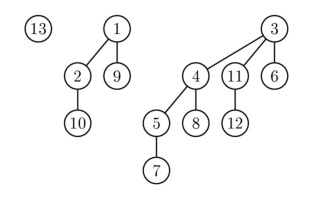

Определение:

Грамматика называется однозначной, если у каждого слова имеется не более одного дерева разбора в этой грамматкие.

Утверждение:

Пусть [math]\Gamma[/math] - однозначная грамматика. Тогда [math]\forall \omega \in \mathbb{L}(\Gamma)[/math] у [math]\omega[/math] существует ровно один левосторонний (правосторонний) вывод.

[math]\triangleright[/math]

Очевидно, что по дереву разбора однозначно восстанавливается левосторонний вывод. Поскольку каждое слова из языка выводится только одним деревом разбора, то и левосторонний вывод, выводящий это слово, существует только один

[math]\triangleleft[/math]