Прямое произведение ДКА — различия между версиями
Kris (обсуждение | вклад) м |
Kris (обсуждение | вклад) м |
||
| Строка 18: | Строка 18: | ||
Согласно определению: | Согласно определению: | ||
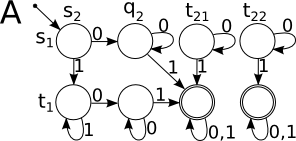
| − | + | #<tex>\Sigma = \lbrace 0, 1 \rbrace</tex> | |
| − | + | #<tex>Q = \lbrace \langle s_1, s_2 \rangle, \langle s_1, q_2 \rangle, \langle s_1, t_{21} \rangle, \langle s_1, t_{22} \rangle, \langle t_1, s_2 \rangle, \langle t_1, q_2 \rangle, \langle t_1, t_{21} \rangle, \langle t_1, t_{21} \rangle \rbrace</tex> | |
| − | + | #<tex>s = \langle s_1, s_2 \rangle</tex> | |
| − | + | #<tex>T = \lbrace \langle t_1, t_{21} \rangle, \langle t_1, t_{22} \rangle \rbrace</tex> | |
| − | *<tex>\delta(\langle s_1, s_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(s_2, 0) \rangle = \langle s_1, q_2 \rangle </tex> | + | #<tex>\delta :</tex> |
| − | *<tex>\delta(\langle s_1, s_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(s_2, 1) \rangle = \langle t_1, s_2 \rangle </tex> | + | #*<tex>\delta(\langle s_1, s_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(s_2, 0) \rangle = \langle s_1, q_2 \rangle </tex> |
| − | *<tex>\delta(\langle s_1, q_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(q_2, 0) \rangle = \langle s_1, q_2 \rangle </tex> | + | #*<tex>\delta(\langle s_1, s_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(s_2, 1) \rangle = \langle t_1, s_2 \rangle </tex> |
| − | *<tex>\delta(\langle s_1, q_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(q_2, 1) \rangle = \langle t_1, t_{21} \rangle </tex> | + | #*<tex>\delta(\langle s_1, q_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(q_2, 0) \rangle = \langle s_1, q_2 \rangle </tex> |
| − | *.. | + | #*<tex>\delta(\langle s_1, q_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(q_2, 1) \rangle = \langle t_1, t_{21} \rangle </tex> |
| − | + | #*... | |
| − | |||
== Применение == | == Применение == | ||
Изменив конструкцию, можно получить автомат допускающий разность или объединение двух языков. | Изменив конструкцию, можно получить автомат допускающий разность или объединение двух языков. | ||
=== Объединение ДКА === | === Объединение ДКА === | ||
| + | [[Файл:Multi_DKA_united.png]] | ||
| − | Необходимо разрешать любую цепочку удовлетворяющую первому или второму автомату, для этого пометим терминальными следующие вершины <tex>T = (T_1 \times | + | Необходимо разрешать любую цепочку удовлетворяющую первому или второму автомату, для этого пометим терминальными следующие вершины <tex>T = (T_1 \times Q_2) \cup (Q_1 \times T_2)</tex>. Полученный автомат удовлетворяет нашим требованиям так как попав в какое-либо состояние из <tex>T_1</tex> или <tex>T_2</tex>, цепочка начинает удовлетворять первому или второму автомату соответственно. |
=== Разность ДКА === | === Разность ДКА === | ||
Версия 00:19, 9 октября 2014
| Определение: |
| Прямым произведением двух ДКА и называется ДКА , где:
|
Содержание
Пример
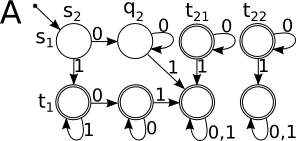
Возьмем автомат , и автомат .
Автомат будет их пересечением.
Согласно определению:
-
- ...
Применение
Изменив конструкцию, можно получить автомат допускающий разность или объединение двух языков.
Объединение ДКА
Необходимо разрешать любую цепочку удовлетворяющую первому или второму автомату, для этого пометим терминальными следующие вершины . Полученный автомат удовлетворяет нашим требованиям так как попав в какое-либо состояние из или , цепочка начинает удовлетворять первому или второму автомату соответственно.
Разность ДКА
- С помощью данной конструкции можно построить автомат для пересечения регулярных языков.