Двоичный каскадный сумматор — различия между версиями
Tanfilyev (обсуждение | вклад) |
Tanfilyev (обсуждение | вклад) |
||
| Строка 9: | Строка 9: | ||
<Br/> | <Br/> | ||
<Br/> | <Br/> | ||
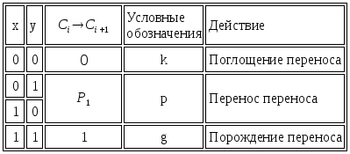
| + | Построим таблицу зависимости <tex>C_{i+1}</tex> от <tex>X_{i}, Y_{i}, C_{i}</tex>, и введем условные обозначения: | ||
| + | <Br/>[[Файл:Таблица_истиности_для_полного_сумматора.png|350px]] | ||
<Br/> | <Br/> | ||
| − | |||
| − | |||
| − | |||
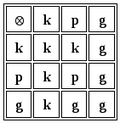
Обозначим композицию действий над переносами значком <tex>\bigotimes</tex> и рассмотрим таблицу: | Обозначим композицию действий над переносами значком <tex>\bigotimes</tex> и рассмотрим таблицу: | ||
| + | <Br/>[[Файл:Таблица_истинности_для_композиции.png|120px]] | ||
<Br/> | <Br/> | ||
| + | Пример: | ||
| + | <Br/>[[Файл:Пример компазиции.png|430px]] | ||
<Br/> | <Br/> | ||
| + | Таким образом функцию <tex>\bigotimes</tex> можно определить как последнее не "P" | ||
| + | |||
| + | Пусть <tex>f_{i}\epsilon \left \{k,p,g\right \}</tex>, тогда: <tex>f_{i}=(f_{1}\bigotimes f_{2}\bigotimes f_{3}\bigotimes...\bigotimes f_{i})_{(0)}</tex>. | ||
| + | |||
| + | Пусть элемент | ||
| + | [[Файл:Первый_элемент.png|130px|left]] | ||
| + | <Br/>возвращает <tex>\bigotimes</tex> двух функций, а | ||
| + | [[Файл:Второй_элемент.png|130px|left]] | ||
| + | <Br/>Возврощает <tex>C'</tex>, старший бит сумматора. | ||
<Br/> | <Br/> | ||
<Br/> | <Br/> | ||
<Br/> | <Br/> | ||
| − | + | dd | |
| − | |||
| − | |||
| − | |||
Версия 05:07, 15 октября 2010
Эта статья находится в разработке!
Рассмотрим один элемент полного сумматора:
Построим таблицу зависимости от , и введем условные обозначения:
Обозначим композицию действий над переносами значком и рассмотрим таблицу:
Пример:
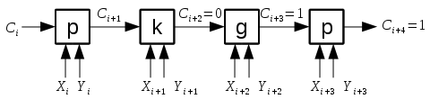
Таким образом функцию можно определить как последнее не "P"
Пусть , тогда: .
Пусть элемент
возвращает двух функций, а
Возврощает , старший бит сумматора.
dd