|
|
| Строка 22: |
Строка 22: |
| | | | |
| | ==Пример== | | ==Пример== |
| − | Задан неориентированный связный граф, требуется построить в нём минимальное остовное дерево.
| + | Рассмотрим работу алгоритма на примере графа. |
| − | * Создадим новый граф, содержащий все вершины из заданного графа, но не содержащий рёбер.
| |
| − | * Этот новый граф будет ответом, его множество рёбер будет изменено по ходу выполнения алгоритма.
| |
| − | * Создадим новое множество вершин с внешними значениями - приоритетами, из которого будем извлекать минимум.
| |
| − | * Заполним все приоритеты этого множества бесконечностью.
| |
| − | * Выберем произвольную вершину, от которой будет начато построение минимального остовного дерева (в примере это вершина '''a''').
| |
| − | * Установим приоритет этой вершины равный нулю.
| |
| | {| cellpadding = "20" class = "wikitable" | | {| cellpadding = "20" class = "wikitable" |
| | ! Изображение !! Множество вершин !! Описание | | ! Изображение !! Множество вершин !! Описание |
Версия 21:13, 11 октября 2014
Алгоритм Прима(англ. Prim's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.
Идея
Данный алгоритм очень похож на алгоритм Дейкстры. Будем последовательно строить поддерево [math]F[/math] ответа в графе [math]G[/math], поддерживая приоритетную очередь [math]Q[/math] из вершин [math]G \setminus F[/math], имеющую ключом для вершины [math]v[/math] величину [math]\min\limits_{u \in VF, uv \in EG}w(uv)[/math] — вес минимального ребра из вершин [math]F[/math] в вершину [math]v[/math]. Также для каждой вершины очереди будем хранить [math]p(v)[/math] — вершину [math]u[/math], на которой достигается минимум в определении ключа. Дерево [math]F[/math] поддерживается неявно, и его ребра — это пары [math]\left(v,p(v)\right)[/math], где [math]v \in G \setminus \{r\} \setminus Q[/math], а [math]r[/math] — корень [math]F[/math]. Изначально [math]F[/math] пусто, в очереди все вершины с ключами [math]+\infty[/math]. Выберём произвольную вершину [math]r[/math] и присвоим её ключу значение [math]0[/math]. На каждом шаге будем извлекать минимальную вершину [math]v[/math] из приоритетной очереди и релаксировать все ребра [math]vu[/math], такие что [math]u \in Q[/math], выполняя при этом операцию [math]\text{decreaseKey}[/math] над очередью и обновление [math]p(v)[/math]. Ребро [math]\left(v,p(v)\right)[/math] при этом добавляется к ответу.
Реализация
function Prim(G, w)
for v [math]\in[/math] V[G]
key[v] [math]\leftarrow \infty [/math]
p[v] [math]\leftarrow[/math] NIL
r [math]\leftarrow [/math] произвольная вершина в V[G]
key[r] [math]\leftarrow[/math] 0
Q [math]\leftarrow[/math] V[G]
while Q [math]\neq \emptyset [/math]
v [math]\leftarrow[/math] extractMin(Q)
for u [math]\in[/math] Adj[v]
if u [math]\in[/math] Q and key[u] > w(v, u)
[math] p[u] \leftarrow v [/math]
key[u] [math]\leftarrow[/math] w(v, u)
decreaseKey(Q, u, key[u])
Ребра дерева восстанавливаются из его неявного вида после выполнения алгоритма.
Пример
Рассмотрим работу алгоритма на примере графа.
| Изображение |
Множество вершин |
Описание
|
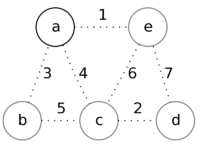
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math]\infty[/math] |
[math]\infty[/math] |
[math]\infty[/math] |
[math]\infty[/math]
|
|
Извлечём из множества вершину a, так как её приоритет минимален.
Рассмотрим смежные с ней вершины b, c, и e.
Обновим их приоритеты, как веса соответствующих рёбер ab, ac и ae, которые будут добавленны в ответ.
|
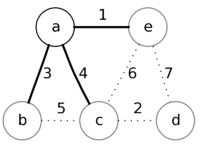
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math] 3 [/math] |
[math] 4 [/math] |
[math]\infty[/math] |
[math] 1 [/math]
|
|
Теперь минимальный приоритет у вершины е.
Извлечём её и рассмотрим смежные с ней вершины a, c, и d.
Изменим приоритет только у вершины d, так как приоритеты вершин a и с меньше,
чем веса у соответствующих рёбер ea и ec, и установим приоритет вершины d равный весу ребра ed, которое будет добавленно в ответ.
|
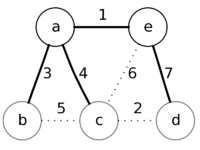
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math] 3 [/math] |
[math] 4 [/math] |
[math] 7 [/math] |
[math] 1 [/math]
|
|
После извлечения вершины b ничего не изменится, так как приоритеты вершин a и с меньше,
чем веса у соответствующих рёбер ba и bc. Однако, после извлечения следующей вершины - c,
будет обновлён приоритет у вершины d на более низкий (равный весу ребра cd) и в ответе ребро ed будет заменено на cd.
|
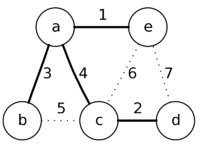
|
| a |
b |
c |
d |
e
|
| [math] 0 [/math] |
[math] 3 [/math] |
[math] 4 [/math] |
[math] 2 [/math] |
[math] 1 [/math]
|
|
Далее будет рассмотрена следующая вершина - d, но ничего не изменится,
так как приоритеты вершин e и с меньше, чем веса у соответствующих рёбер de и dc.
После этого алгоритм завершит работу, так как в заданном множестве не останется вершин,
которые не были бы рассмотрены
|
Корректность
По поддерживаемым инвариантам после извлечения вершины [math]v[/math] ([math]v \neq r[/math]) из [math]Q[/math] ребро [math]\left(v,p(v)\right)[/math] является ребром минимального веса, пересекающим разрез [math]\left(F,Q\right)[/math]. Значит, по лемме о безопасном ребре, оно безопасно. Алгоритм построения MST, добавляющий безопасные ребра, причём делающий это ровно [math]|V|-1[/math] раз, корректен.
Оценка производительности
Производительность алгоритма Прима зависит от выбранной реализации приоритетной очереди, как и в алгоритме Дейкстры. Извлечение минимума выполняется [math]V[/math] раз, релаксация — [math]O(E)[/math] раз.
| Структура данных для приоритетной очереди
|
Асимптотика времени работы
|
| Наивная реализация
|
[math]O(V^2+E)[/math]
|
| Двоичная куча
|
[math]O(E\log{V})[/math]
|
| Фибоначчиева куча
|
[math]O(V\log{V}+E)[/math]
|
См. также
Источники информации



