Двоичный каскадный сумматор

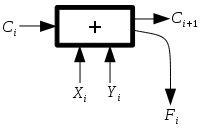
Рассмотрим один элемент полного сумматора:

Где [math]X_{i}, Y_{i}[/math] - i-ный разряд суммируемых чисел, [math]C_{i}, C_{i+1}[/math] - Биты переноса, а [math]F_{i}[/math] - Результат сложения.

Построим таблицу зависимости [math]C_{i+1}[/math] от [math]X_{i}, Y_{i}, C_{i}[/math], и введем условные обозначения:

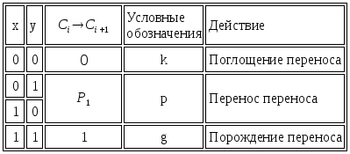
Обозначим композицию действий над переносами значком [math]\bigotimes[/math] и рассмотрим таблицу:

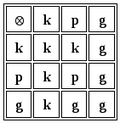
Пример:

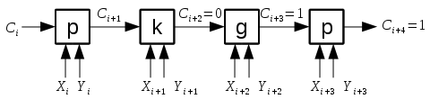
Таким образом функцию [math]\bigotimes[/math] можно определить как последнее не "P".

Пусть [math]f_{i}\epsilon \left \{k,p,g\right \}[/math], тогда: [math]C_{i}=(f_{1}\bigotimes f_{2}\bigotimes f_{3}\bigotimes...\bigotimes f_{i})_{(0)}[/math].

Пусть элемент возвращает [math]\bigotimes[/math] двух функций,
а элемент 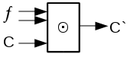возвращает [math]C'[/math], старший бит сумматора.

Схема двоичного каскадного сумматора выглядит следующим образом:
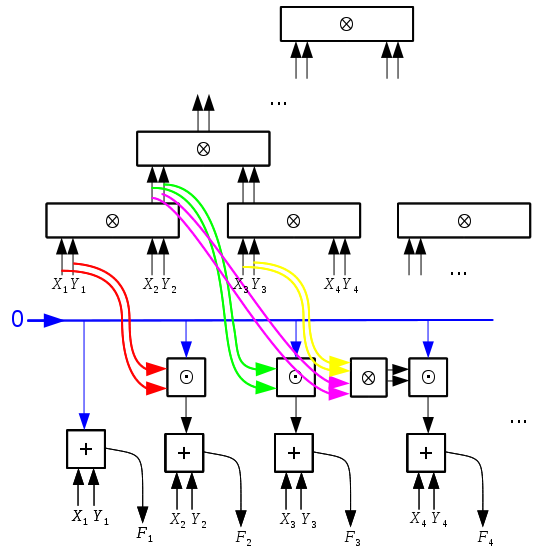
Сумматор состоит из двух частей. Первой частью является дерево отрезков [1], с помощью которого, вычисляется бит переноса. Вторая часть это группа полных сумматоров, вычисляющих ответ.