Матричный умножитель — различия между версиями
(→Вычисление частичных произведений) |
|||
| Строка 1: | Строка 1: | ||
== Определение == | == Определение == | ||
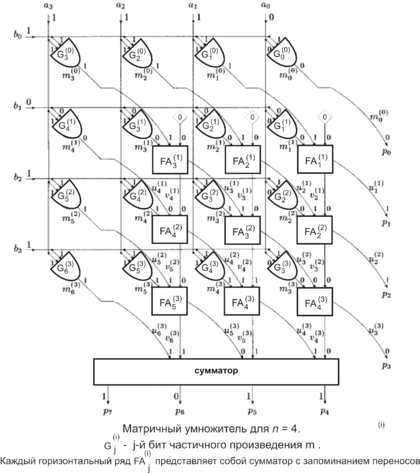
| + | [[Файл:Рисунок2.png|420px|thumb|right]] | ||
Матричный умножитель - цифровая схема, осуществляющяя умножение двух чисел. | Матричный умножитель - цифровая схема, осуществляющяя умножение двух чисел. | ||
| Строка 8: | Строка 9: | ||
Матричный умножитель вычисляет частичные произведения по формуле: <br> | Матричный умножитель вычисляет частичные произведения по формуле: <br> | ||
<math>m^{(i)} = a * b_i * 2^{i}</math> | <math>m^{(i)} = a * b_i * 2^{i}</math> | ||
| − | |||
==== Суммирование частичных произведений ==== | ==== Суммирование частичных произведений ==== | ||
Версия 08:43, 15 октября 2010
Содержание
Определение
Матричный умножитель - цифровая схема, осуществляющяя умножение двух чисел.
Принцип работы
Вычисление частичных произведений
Матричный умножитель вычисляет частичные произведения по формуле:
Суммирование частичных произведений
На этом этапе происходит сложение всех частичных произведений m. Это происходит так: вначале мы суммируем и , саму сумму занесем в , а переносы в (в и будет не более n+1 битов в каждом), затем суммируем числа , , и получаем , . Так суммируется , , для всех i = 2, 3, … , n – 1. В итоге получаем два числа и , которые складываем с помощью двоичного каскадного сумматора.
Схемная сложность
Частичные произведения вычисляются за n шагов, то есть имеют временную сложность O(n). Сложение с вычисление переносов включает n - 1 шагов и требут времени O(n). Последнее сложение можно выполнить за O(log n).
В итоге суммарное время работы:
O(n) + O(n) + O(log n) = O(n)
Есть и более быстрые способы умножения двух чисел, например умножение с помощью дерева Уоллеса, которое работает O(log n).