Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний

Постановка задачи

Пусть дан автомат [math]A[/math]. Требуется построить автомат [math]A_{min}[/math] с наименьшим количеством состояний, распознающий тот же язык, что и [math]A[/math].

Алгоритм

Описание

Основная идея алгоритма заключается в том, чтобы разбить состояния на классы эквивалентности — они и будут состояниями минимизированного автомата.

Для реализации алгоритма нам потребуются очередь [math]Q[/math] и таблица [math]marked[/math] размером [math]n \times n[/math], где [math]n[/math] — количество состояний автомата. Будем помечать в таблице пары неэквивалентных состояний и класть их в очередь.

• Удобно будем добавить в исходный автомат вершину [math]0[/math], в которую будут вести по умолчанию все переходы по всем символам, которых ещё не было в исходном автомате. Теперь стартовое состояние будет иметь номер [math]1[/math].
• Шаг 1. Построим множество [math]\delta^{-1}[/math], в котором будем хранить списки обратных ребер.
• Шаг 2. Найдем все достижимые состояния из стартового.
• Шаг 3. Добавим в очередь [math]Q[/math] пары состояний, различимых строкой [math] \varepsilon [/math], и пометим их в таблице.
• Шаг 4. Для каждой непомеченной пары [math] \langle u, v \rangle [/math] нужно проверить, что [math]\mathcal {9} c \in \Sigma[/math] такой, что пара [math]\langle \delta(u, c), \delta(v, c) \rangle[/math] помечена. Тогда мы можем пометить пару [math] \langle u, v \rangle [/math].

Пока [math]Q[/math] не станет пуста, будем делать следующее:

1. Извлечем пару [math] \langle u, v \rangle [/math] из [math]Q[/math].

2. Для каждого символа [math]c \in \Sigma[/math] перебираем пары состояний [math]\langle \delta^{-1}(u, c), \delta^{-1}(v,c) \rangle[/math]. Если находим ещё непомеченную пару, то помечаем её в таблице и кладем в очередь.

В момент опустошения очереди пары состояний, не помеченные в таблице, являются парами эквивалентных состояний.

• Шаг 5. За один проход по таблице разбиваем пары эквивалентных состояний на классы эквивалентности.
• Шаг 6. За один проход по списку классов эквивалентности выделяем список новых состояний и переходов между ними.

Стартовым состоянием полученного автомата будет состояние, соответствующее классу эквивалентности, содержащему стартовое состояние исходного автомата.

Терминальными состояниями полученного автомата будут состояния, соответствующие классам эквивалентности, содержащим терминальные состояния исходного автомата.

Корректность

Пусть в результате применения данного алгоритма к автомату [math]A[/math] мы получили автомат [math]A_{min}[/math]. Докажем, что этот автомат минимальный и единственный с точностью до изоморфизма.

Пусть существует автомат [math]A'[/math], эквивалентный [math]A[/math], но с числом состояний меньшим, чем в [math]A_{min}[/math]. Стартовые состояния [math]s \in A_{min}[/math] и [math]s' \in A'[/math] эквивалентны, так как [math]A_{min}[/math] и [math]A'[/math] допускают один и тот же язык. Рассмотрим строку [math]\alpha = a_1a_2...a_{k}[/math], где [math]a_{i} \in \Sigma[/math], такую, что [math] \langle s, \alpha \rangle \vdash^* \langle u, \varepsilon \rangle [/math], [math] \langle s', \alpha \rangle \vdash^* \langle u', \varepsilon \rangle [/math]. Пусть [math]\langle s, a_1 \rangle \vdash^* \langle l, \varepsilon \rangle [/math] и [math]\langle s', a_1 \rangle \vdash^* \langle l', \varepsilon \rangle [/math]. Так как [math]s[/math] и [math]s'[/math] эквивалентны, то [math]l[/math] и [math]l'[/math] эквивалентны. Аналогично для всех [math]a_{i}[/math]. В итоге получим, что [math]u[/math] эквивалентно [math]u'[/math]. Значит, для каждого состояния из [math]A_{min}[/math] существует эквивалентное состояние из [math]A'[/math].

Состояний в [math]A'[/math] меньше, чем в [math]A_{min}[/math], значит двум состояниям из [math]A_{min}[/math] эквивалентно одно состояние из [math]A'[/math]. Тогда эти два состояния эквивалентны, но автомат [math]A_{min}[/math] построен так, что в нем нет эквивалентных состояний. Противоречие.

Так как каждому состоянию из [math]A_{min}[/math] эквивалентно состояние из [math]A'[/math], то автоматы [math]A_{min}[/math] и [math]A'[/math] изоморфны.

Псевдокод

Функция для построения списка обратных ребер.

vector[][] buildReverseEdges(int n, int[][] [math]\delta[/math]):
   int [math]\delta^{-1}[/math][n][n]
   for i = 0 .. n - 1
      for c [math]\in[/math] [math]\Sigma[/math]
         [math]\delta^{-1}[/math][[math]\delta[/math][i][c]][c].add(i)
   return [math]\delta^{-1}[/math]

Функция для проверки достижимости состояний.

function checkReachability(int u, boolean[] visited):
   visited[u] = true;
   for c [math]\in[/math] [math]\Sigma[/math]
      if not visited[[math]\delta[/math][u][c]]
         checkReachability([math]\delta[/math][u][c], visited)

Функция для инициализации таблицы неэквивалентности.

function initTable(int n, boolean[] isTerminal, queue Q, boolean[][] marked):
   for i = 0 .. n - 1
      for j = 0 .. n - 1
         if not marked[i][j] and isTerminals[i] and not isTerminals[j] and i != j
            marked[i][j] = marked[j][i] = true
            Q.push([math]\langle i, j \rangle[/math])

Функция для вычисления таблицы неэквивалентности.

function computeTable(int n, int[][] [math]\delta^{-1}[/math], queue Q, boolean[][] marked):
   while not Q.isEmpty()
      [math]\langle u, v \rangle[/math] = Q.poll()
      for c [math]\in[/math] [math]\Sigma[/math]
         list rr = [math]\delta^{-1}[/math][u][c]
         list ss = [math]\delta^{-1}[/math][v][c]	
         for i = 0 .. length(rr) - 1
            int r = rr[i]
            for j = 0 .. length(ss) - 1
               int s = ss[j]
               if not marked[r][s]
                  marked[r][s] = marked[s][r] = true
                  Q.push([math]\langle r, s \rangle[/math])

Основная функция алгоритма.

function minimization(int n, boolean[] isTerminal, int[][] [math]\delta[/math]):
   // Шаг 1
   int[][] [math]\delta^{-1}[/math] = buildReverseEdges(n, [math]\delta[/math])
   // Шаг 2
   boolean reachable[n]
   checkReachability(1, reachable) 
   // Шаг 3
   queue Q
   boolean marked[n][n]
   initTable(n, isTerminal, Q, marked)
   // Шаг 4
   computeTable(n, [math]\delta^{-1}[/math], Q, marked)
   // Шаг 5
   int[] component[n] // По позиции i будем хранить номер компоненты эквивалентности для i-ого состояния.
   fill(component, -1)
   list classes // По позиции i будем хранить представителя i-ой компоненты эквивалентности.
   for i = 0 .. n - 1
      if not table[0][i]
         component[i] = 0
	
   int components_count = 0
   for i = 1 .. n - 1
      if not visited[i]
         continue
      if component[i] == -1
         components_count++
         component[i] = components_count
         classes.add(i)
         for j = i + 1 .. n - 1
            if not table[i][j]
               component[j] = components_count
   // Шаг 6
   for i = 0 .. length(classes) - 1
      int u = component[classes[i]]
      for c [math]\in[/math] [math]\Sigma[/math]
         if reachable[[math]\delta[/math][classes[i]][c]] and component[[math]\delta[/math][classes[i]][c]] != 0
            int v = component[[math]\delta[/math][classes[i]][c]]
            output(u ->[c]-> v) // Ребро из u в v по символу c

Асимптотики

Каждую пару мы добавляли в очередь один раз, значит время заполнения таблицы [math]O(n^2)[/math]. Разбиение на классы эквивалентности делается за один проход по таблице, то есть за [math]O(n^2)[/math].

Пример работы

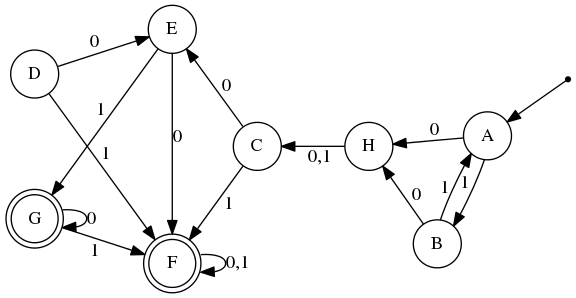
Минимизируем данный автомат.

Будем рассматривать только нижний треугольник таблицы пар различимых состояний.

Отметили состояния, различающиеся строкой [math]\varepsilon[/math]:

B
C
D
E
F	x	x	x	x	x
G	x	x	x	x	x
H						x	x
	A	B	C	D	E	F	G

На момент опустошения очереди:

B
C	x	x
D	x	x
E	x	x	x	x
F	x	x	x	x	x
G	x	x	x	x	x
H	x	x	x	x	x	x	x
	A	B	C	D	E	F	G

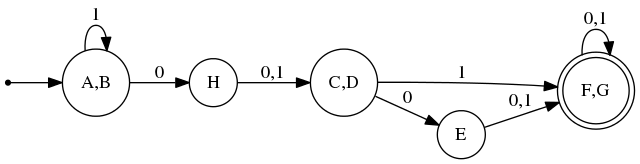
Из таблицы видно, что классы эквивалентных состояний это [math] \mathcal {f} A, B \mathcal {g}, \mathcal {f} C, D \mathcal {g}, \mathcal {f} F, G \mathcal {g}, \mathcal {f} E \mathcal {g}, \mathcal {f} H \mathcal {g} [/math].

Итого получили такой автомат:

Источники информации

• Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е издание. Пер. с англ. — М.: Издательский дом «Вильямс», 2002. — С. 171 - 182. — ISBN 5-8459-0261-4
• Wikipedia:DFA_minimization
• Minimization of DFAs
• DFA Minimization