Алгоритм Кока-Янгера-Касами разбора грамматики в НФХ — различия между версиями
Kabanov (обсуждение | вклад) м |
Kabanov (обсуждение | вклад) м |
||
| Строка 43: | Строка 43: | ||
== См. также == | == См. также == | ||
| + | * [[Алгоритм Кока-Янгера-Касами, модификация для произвольной грамматики|Алгоритм Кока-Янгера-Касами, модификация для произвольной грамматики]] | ||
| + | * [[Алгоритм_Эрли|Алгоритм Эрли]] | ||
==Источники информации== | ==Источники информации== | ||
| + | * [[wikipedia:CYK_algorithm|Wikipedia {{---}} CYK algorithm]] | ||
| + | * [http://web.cs.ucdavis.edu/~rogaway/classes/120/winter12/CYK.pdf David Rodriguez-Velazquez, "The CYK Algorithm"] | ||
| + | * [https://www.princeton.edu/~achaney/tmve/wiki100k/docs/CYK_algorithm.html Princeton University, "The CYK Algorithm"] | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
Версия 22:10, 4 ноября 2014
| Задача: |
| Пусть дана контекстно-свободная грамматика грамматика в нормальной форме Хомского и слово . Требуется выяснить, выводится ли это слово в данной грамматике. |
Алгоритм
Описание
Пусть , если из нетерминала можно вывести подстроку . Иначе :
.
Будем динамически заполнять матрицу следующим алгоритмом (индукция по ):
- База. . Ячейки заполняются значением , если правило принадлежит множеству правил грамматики : .
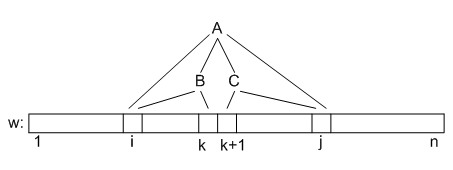
- Переход. Рассмотрим все пары . Значения для всех нетерминалов и пар уже вычислены, так что: .
- Завершение. После окончания работы ответ содержится в ячейке , где .
Псевдокод
Асимптотика
Необходимо вычислить булевых величин. На каждую требуется затратить операций, где – количество правил. Суммируя по всем правилам получаем конечную сложность .
Алгоритму требуется памяти, где — количество нетерминалов грамматики.
Пусть, - длина входной строки, а - количество правил вывода в грамматике.
Обработка правил вида выполняется за .
Проход по всем подстрокам выполняется за . В обработке подстроки присутствует цикл по всем правилам вывода и по всем разбиениям на две подстроки, следовательно обработка работает за . В итоге - .
Следовательно, общее время работы алгоритма - . Кроме того, алгоритму требуется память (на массив ) объемом .
Недостаток алгоритма заключается в том, что изначально грамматику необходимо привести к НФХ.