Алгоритм Кока-Янгера-Касами разбора грамматики в НФХ

Задача:

Пусть дана контекстно-свободная грамматика грамматика [math]\Gamma[/math] в нормальной форме Хомского и слово [math]w \in \Sigma^{*}[/math]. Требуется выяснить, выводится ли это слово в данной грамматике.

Алгоритм

Описание

Пусть [math]a_{A, i, j} = true[/math], если из нетерминала [math]A[/math] можно вывести подстроку [math]w[i..j][/math]. Иначе [math]a_{A, i, j} = false[/math]:

[math]a_{A, i, j} = \begin{cases} true,&\text{$A \Rightarrow^{*} w[i..j]$;}\\ false,&\text{else.} \end{cases} [/math].

Будем динамически заполнять матрицу [math]a_{A, i, j}[/math] следующим алгоритмом (индукция по [math]m = j - i[/math]):

• База. [math]m = 0[/math]. Ячейки [math]a_{A, i, i}[/math] заполняются значением [math]true[/math], если правило [math]A \rightarrow w[i][/math] принадлежит множеству правил [math]P[/math] грамматики [math]\Gamma[/math]: [math]a_{A, i, i} = \lbrack A \rightarrow w[i] \in P \rbrack[/math].

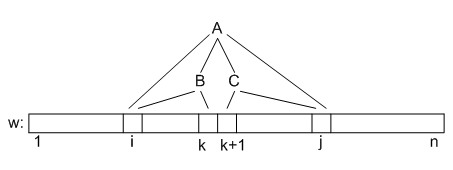
• Переход. Рассмотрим все пары [math]\lbrace \langle j, i \rangle | j-i=m \rbrace[/math]. Значения для всех нетерминалов и пар [math]\lbrace \langle j', i' \rangle | j-i\lt m \rbrace[/math] уже вычислены, так что: [math]a_{A, i, j} = \bigvee\limits_{k=i}^{j-1} \bigvee\limits_{A \rightarrow BC} \left( a_{B, i, k} \wedge a_{C, k+1, j} \right)[/math].

• Завершение. После окончания работы ответ содержится в ячейке [math]a_{S, 1, n}[/math], где [math]n = |w|[/math].

Псевдокод

boolean CYK(char[] w, list [math]\Gamma[/math], int S)
   int n = length(w)
   boolean d[[math]|\Gamma|[/math]][n][n]
   for i = 1 ... n
      for (A [math]\rightarrow[/math] w[i] [math]\in[/math] [math]\Gamma[/math])
         d[A,i,i] = true
   for len = 1 .. n - 1
      for i = 1 .. n - len
         for (A [math]\rightarrow[/math] BC [math]\in[/math] [math]\Gamma[/math])
            for k = i .. i + len - 1
               d[A][i][i + len] = d[A][i][i + len] or d[B][i][k] and d[C][k + 1][i + len]
return d[S][1][n]

Асимптотика

Необходимо вычислить [math]n^2[/math] булевых величин. На каждую требуется затратить [math]n \cdot |P_A|[/math] операций, где [math]|P_A|[/math] – количество правил. Суммируя по всем правилам получаем конечную сложность [math]O \left( n^3 \cdot |\Gamma| \right)[/math].

Алгоритму требуется [math]n^2 \cdot |N|[/math] памяти, где [math]|N|[/math] — количество нетерминалов грамматики.

Пусть, [math]n[/math] - длина входной строки, а [math]m[/math] - количество правил вывода в грамматике.

Обработка правил вида [math]A \rightarrow a_i[/math] выполняется за [math]O(nm)[/math].

Проход по всем подстрокам выполняется за [math]O(n^2)[/math]. В обработке подстроки присутствует цикл по всем правилам вывода и по всем разбиениям на две подстроки, следовательно обработка работает за [math]O(nm)[/math]. В итоге - [math]O(n^3 m)[/math].

Следовательно, общее время работы алгоритма - [math]O(n^3 m)[/math]. Кроме того, алгоритму требуется память (на массив [math]d[/math]) объемом [math]O(n^2 m)[/math].

Недостаток алгоритма заключается в том, что изначально грамматику необходимо привести к НФХ.

См. также

• Алгоритм Кока-Янгера-Касами, модификация для произвольной грамматики
• Алгоритм Эрли

Источники информации

• Wikipedia — CYK algorithm
• David Rodriguez-Velazquez, "The CYK Algorithm"
• Princeton University, "The CYK Algorithm"