Алгоритм Кока-Янгера-Касами разбора грамматики в НФХ — различия между версиями
Kabanov (обсуждение | вклад) м (→Асимптотика) |
Kabanov (обсуждение | вклад) (→Пример работы) |
||
| Строка 46: | Строка 46: | ||
Дано слово <tex>w = $()(())$</tex>. | Дано слово <tex>w = $()(())$</tex>. | ||
| + | |||
| + | {| clear="both" |} | ||
| + | |||
| + | Инициализация массива <tex>d</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
| + | {| clear="both" |} | ||
| + | |||
| + | Заполнение массива <tex>d</tex>. | ||
| + | |||
| + | {| clear="both" |} | ||
| + | |||
| + | Итерация m = <tex>1</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
| + | |||
| + | Итерация m = <tex>2</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
| + | |||
| + | Итерация m = <tex>3</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
| + | |||
| + | Итерация m = <tex>4</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
| + | |||
| + | Итерация m = <tex>5</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
| + | |||
| + | Итерация m = <tex>6</tex>. | ||
| + | |||
| + | |||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|A | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|B | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|C | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| + | ! colspan="7"|D | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |} | ||
| + | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | ||
| + | ! colspan="7"|E | ||
| + | |- | ||
| + | ! | ||
| + | ! 1 | ||
| + | ! 2 | ||
| + | ! 3 | ||
| + | ! 4 | ||
| + | ! 5 | ||
| + | ! 6 | ||
| + | |- | ||
| + | ! 1 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 2 | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 3 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 4 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 5 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | | | ||
| + | |||
| + | |- | ||
| + | ! 6 | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | align="center"| ● | ||
| + | |||
| + | |} | ||
| + | {| clear="both" |} | ||
== См. также == | == См. также == | ||
Версия 02:14, 5 ноября 2014
| Задача: |
| Пусть дана контекстно-свободная грамматика в нормальной форме Хомского и слово . Требуется выяснить, выводится ли это слово в данной грамматике. |
Содержание
Алгоритм
Алгоритм Кока-Янгера-Касами (англ. Cocke-Younger-Kasami algorithm, англ. CYK - алгоритм) — универсальный алгоритм, позволяющий по слову узнать, выводимо ли оно в заданной КС-грамматике в нормальной форме Хомского. Будем решать задачу динамическим программированием. Дана строка размером . Заведем для неё трехмерный массив размером , состоящий из логических значений, и тогда и только тогда, когда из нетерминала правилами грамматики можно вывести подстроку .
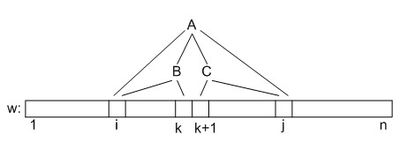
Рассмотрим все пары , где — константа и .
- . Инициализируем массив для всех нетерминалов, из которых выводится какой-либо символ строки . В таком случае , если в грамматике присутствует правило . Иначе .
- . Значения для всех нетерминалов и пар уже вычислены, поэтому . То есть, подстроку можно вывести из нетерминала , если существует продукция вида и такое , что подстрока выводима из , а подстрока выводится из .
После окончания работы значение содержит ответ на вопрос, выводима ли данная строка в данной грамматике, где — начальный символ грамматики.
Модификации
Количество способов вывести слово
Если массив будет хранить целые числа, а формулу заменить на , то — количество способов получить подстроку из нетерминала .
Минимальная стоимость вывода слова
Пусть — стоимость вывода по правилу . Тогда, если использовать формулу , то — минимальная стоимость вывода подстроки из нетерминала .
Таким образом, задача о выводе в КС-грамматике в нормальной форме Хомского является обобщением задачи динамического программирования на подотрезке.
Асимптотика
Обработка правил вида в шаге 1 выполняется за .
Проход по всем подстрокам в шаге 2 выполняется за . В обработке одной подстроки присутствует цикл по всем правилам вывода и по всем разбиениям на две подстроки, следовательно обработка работает за . В итоге получаем конечную сложность .
Следовательно, общее время работы алгоритма — . Кроме того, алгоритму требуется память (на массив ) объемом , где — количество нетерминалов грамматики.
Пример работы
Дана грамматика правильных скобочных последовательностей :
Дано слово .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||