Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора

Основные определения

Определение:

Контекстно-свободной грамматикой (англ. сontext-free grammar) называется грамматика, у которой в левых частях всех правил стоят только одиночные нетерминалы.

Определение:

Контекстно-свободный язык (англ. context-free language) — язык, задаваемый контекстно-свободной грамматикой.

Лево- и правосторонний вывод слова

Определение:

Выводом слова (англ. derivation of a word) [math]\alpha[/math] называется последовательность строк, состоящих из терминалов и нетерминалов. Первая строка последовательности состоит из одного стартового нетерминала. Каждая последующая строка получена из предыдущей путем замены любого нетерминала по одному (любому) из правил, а последней строкой в последовательности является слово [math]\alpha[/math].

Пример:

Рассмотрим грамматику, выводящую все правильные скобочные последовательности.

[math]"("[/math] и [math]")"[/math] — терминальные символы;

[math]S[/math] — стартовый нетерминал;

Правила:
[math]S\rightarrow (S)S[/math]
[math]S\rightarrow S(S)[/math]
[math]S\rightarrow \varepsilon[/math]
Выведем слово [math]"(()(()))()"[/math]:
[math]\boldsymbol{S}\Rightarrow (S)\boldsymbol{S} \Rightarrow (S)(\boldsymbol{S})S\Rightarrow(S)()\boldsymbol{S}\Rightarrow(\boldsymbol{S})()\Rightarrow(\boldsymbol{S}(S))()\Rightarrow(S(S)(\boldsymbol{S}))()\Rightarrow(S(S)(\boldsymbol{S}(S)))()\Rightarrow (S(\boldsymbol{S})((S)))()\Rightarrow(\boldsymbol{S}()((S)))()\Rightarrow(()((\boldsymbol{S})))()\Rightarrow(()(()))()[/math]

Определение:

Левосторонний вывод слова (англ. leftmost derivation)[math]\alpha[/math] — вывод, где каждая последующая строка получена из предыдущей путем замены по одному из правил самого левого встречающегося в строке нетерминала.

Определение:

Правосторонним выводом слова (англ. rightmost derivation) [math]\alpha[/math] — вывод, где каждая последующая строка получена из предыдущей путем замены по одному из правил самого правого встречающегося в строке нетерминала.

Рассмотрим левосторонний вывод скобочной последовательности из примера:
[math]\boldsymbol{S}\Rightarrow (\boldsymbol{S})S \Rightarrow ((\boldsymbol{S})S)S\Rightarrow (()\boldsymbol{S})S\Rightarrow(()\boldsymbol{S}(S))S\Rightarrow(()(\boldsymbol{S}))S\Rightarrow(()(\boldsymbol{S}(S)))S\Rightarrow(()((\boldsymbol{S})))S\Rightarrow(()(()))\boldsymbol{S}\Rightarrow(()(()))(\boldsymbol{S})S\Rightarrow(()(()))()\boldsymbol{S}\Rightarrow(()(()))()[/math]

Дерево разбора

Определение:

Деревом разбора грамматики (англ. parse tree) называется дерево, в вершинах которого записаны терминалы или нетерминалы. Все вершины, помеченные терминалами, являются листьями. Все вершины, помеченные нетерминалами, имеют детей. Дети вершины, в которой записан нетерминал, соответствуют раскрытию нетерминала по одному любому правилу (в левой части которого стоит этот нетерминал) и упорядочены так же, как в правой части этого правила.

Определение:

Крона дерева разбора — множество терминальных символов, упорядоченное в соответствии с номерами их достижения при обходе дерева в глубину из корня. Крона дерева разбора представляет из себя слово языка, которое выводит это дерево.

Построим дерево разбора скобочной последовательности из примера.

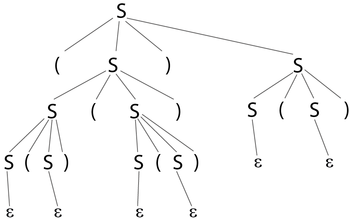
Однозначные грамматики

Определение:

Грамматика называется однозначной (англ. unambiguous grammar), если у каждого слова имеется не более одного дерева разбора в этой грамматике.

Лемма:

Пусть [math]\Gamma[/math] — однозначная грамматика. Тогда [math]\forall \omega \in \mathbb{L}(\Gamma)[/math] существует ровно один левосторонний (правосторонний) вывод.

Доказательство:

[math]\triangleright[/math]

Очевидно, что по дереву разбора однозначно восстанавливается левосторонний(правосторонний) вывод. Поскольку каждое слово из языка выводится только одним деревом разбора, то существует только один левосторонний(правосторонний) вывод этого слова.

[math]\triangleleft[/math]

Утверждение:

Грамматика из примера не является однозначной.

[math]\triangleright[/math]

Выше уже было построено дерево разбора для слова [math]"(()(()))()"[/math]. Построим еще одно дерево разбора для данного слова. Например, оно будет выглядеть так: Таким образом, существует слово, у которого есть более одного дерева разбора в данной грамматике [math]\Rightarrow[/math] эта грамматика не является однозначной.

[math]\triangleleft[/math]

Для одного и того же языка может существовать как однозначная, так и неоднозначная грамматика.

Например, у языка правильных скобочных последовательностей существует однозначная грамматика.

[math]"("[/math] и [math]")"[/math] — терминальные символы;

[math]S[/math] — стартовый нетерминал;

Правила:
[math]S\rightarrow (S)S[/math]
[math]S\rightarrow \varepsilon[/math]

Утверждение:

Грамматика, заданная таким образом является однозначной.

[math]\triangleright[/math]

Как-то очевидно :(

[math]\triangleleft[/math]

Однако, есть КС-языки, для которых не существует однозначных КС-грамматик. Такие языки и грамматики их порождающие называют существенно неоднозначными.

См. также

• Формальные грамматики
• Иерархия Хомского формальных грамматик
• Замкнутость КС-языков относительно различных операций
• Существенно неоднозначные языки

Литература

• Wikipedia — Context-free grammar
• Википедия — Контекстно-свободная грамматика
• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)