Генерация комбинаторных объектов в лексикографическом порядке — различия между версиями
(→Ссылки) |
|||
| Строка 55: | Строка 55: | ||
== Ссылки == | == Ссылки == | ||
* [http://ru.wikipedia.org/wiki/Перечисление_(комбинаторика) Перечисление (комбинаторика)] | * [http://ru.wikipedia.org/wiki/Перечисление_(комбинаторика) Перечисление (комбинаторика)] | ||
| − | * [http://rain.ifmo.ru/cat/view.php/ | + | * [http://rain.ifmo.ru/cat/view.php/ Дискретная математика: алгоритмы] |
* [http://algolist.ru/maths/combinat/ Комбинаторика и переборные задачи] | * [http://algolist.ru/maths/combinat/ Комбинаторика и переборные задачи] | ||
* [http://e-maxx.ru/algo/ Комбинаторика] | * [http://e-maxx.ru/algo/ Комбинаторика] | ||
Версия 13:16, 30 ноября 2014
Содержание
Алгоритм построения
Описание процедуры построения
Данный алгоритм генерирует все объекты заданного типа в лексикографическом порядке. На каждом шаге генерируется минимальный возможный префикс требуемого объекта.
- — процедура генерирования
- — глубина рекурсии
- — текущий комбинаторный объект.
- — требуемый размер объекта
- — все возможные элементы комбинаторного объекта, отсортированные в лексикографическом порядке
- — размер alpha
- — список, содержащий все сгенерированные объекты в нужном порядке
list <A> genObj(K, p)
if p == len // если сформирован объект нужного размера, то возвращаем его
ans.push_back(K); // записываем объект K в ответ
else
for i = 1 to n
if к объекту К можно добавить элемент alpha[i] в конец
K.push_back(alpha[i])
genObj(K, p + 1) // добавляем alpha[i] в конец и вызываем функцию genObj от нового полученного префикса
К.pop_back()
Генерация с помощью процедуры получения следующего объекта
Составляем первый объект — , для него получаем следующий объект — , для получаем , далее действуем также, для получая объект, пока не получим последний объект .
Примеры
Пример генерации сочетаний из N элементов по M в лексикографическом порядке
Данный алгоритм генерирует все сочетания из элементов по .
- — процедура генерирования
- — текущее сочетание
- — следующий элемент в сочетании
- — глубина рекурсии
- — все сгенерированные сочетания в нужном порядке
list <int> genChooses(k, l)
a[l] = k;
if l == m
ans.push_back(a)
for i = k + 1 to n
genChooses(i, l + 1);
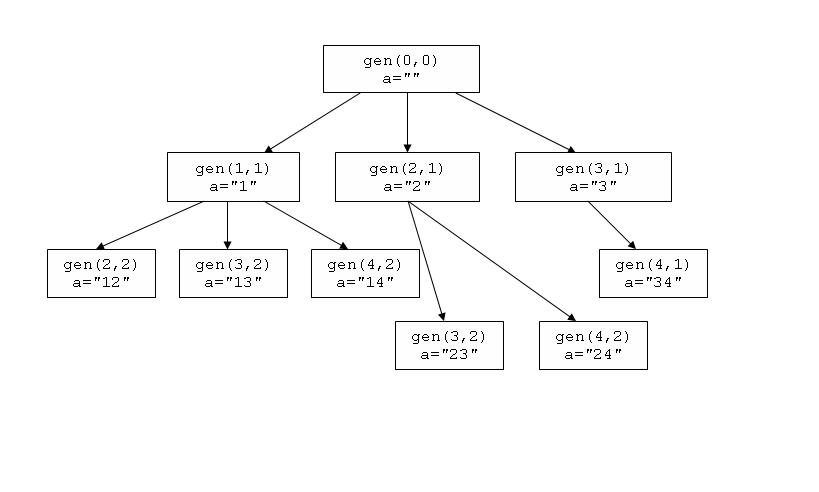
Пример работы процедуры генерации
Иллюстрация работы процедуры генерирования всех сочетаний из 4 по 2.