Представление целых чисел: прямой код, код со сдвигом, дополнительный код

Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:

• не требовал усложнения архитектуры процессора для выполнения арифметических операций с отрицательными числами;
• не усложнял арифметические действия;
• хранил бы одинаковое количество положительных и отрицательных чисел.

Рассмотрим разные методы представления.

Прямой код

Нумерация двоичных чисел в прямом представлении

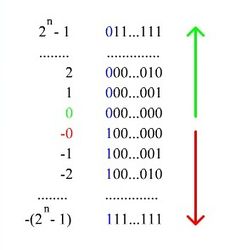
При записи числа в прямом коде (англ. sign-and-magnitude method) старший разряд является знаковым разрядом. Если его значение равно нулю, то число положительное, если единице — отрицательное. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число [math] -5 [/math] в восьмибитном типе данных, использующем прямой код, будет выглядеть так: [math] 10000101 [/math].

Таким способом в [math] n [/math]-битовом типе данных можно представить диапазон чисел [math] [-2^{n-1} + 1; 2^{n-1} - 1] [/math].

Достоинства метода:

• получить прямой код числа достаточно просто.

Недостатки:

• выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого);
• существуют два нуля [math] +0 [/math] и [math] -0 [/math], из-за чего усложняется арифметическое сравнение.

Из-за этого прямой код используется очень редко.

Код со сдвигом

Код со сдвигом. Как видно, двоичное представление зациклено по модулю [math]1000..000_{(2)}[/math] ([math]n[/math] нулей)

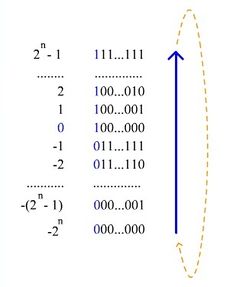
При использовании кода со сдвигом (excess-[math] K [/math], где [math] K = 2^{n-1} [/math]; также говорят biased representation) целочисленный отрезок от нуля до [math] 2^n [/math] ([math] n [/math] — количество бит) сдвигается влево на [math] 2^{n-1} [/math], а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от [math] 000 \dots 0 [/math] до [math] 111 \dots 1 [/math]. Например, число [math] -5 [/math] в восьмибитном типе данных, использующем код со сдвигом, превратится в [math] -5 + 128 = 123 [/math], то есть будет выглядеть так: [math] 01111011 [/math].

По сути, при таком кодировании:

• к кодируемому числу прибавляют [math] 2^{n-1} [/math];
• переводят получившееся число в двоичную систему исчисления.

Можно получить диапазон значений [math] [-2^{n-1}; 2^{n-1} - 1][/math].

Достоинства метода:

• не требуется усложнение архитектуры процессора;
• нет проблемы двух нулей.

Недостатки:

• при арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть);
• ряд положительных и отрицательных чисел несимметричен.

Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.

Дополнительный код (дополнение до единицы)

Нумерация двоичных чисел в представлении c дополнением до единицы. В отличии от кода со сдвигом, нулю соответствуют коды [math] 00...000 [/math] и [math] 11...111 [/math]

В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones' complement).

Алгоритм получения кода числа:

• если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число;
• если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код)

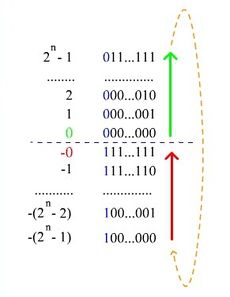
Пример: переведём число [math] -13 [/math] в восьмибитный код (так оно будет храниться в типе данных unsigned int). Прямой код модуля [math] -13 [/math] — [math] 00001101 [/math], инвертируем и получаем [math] 11110010 [/math]. Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.

Таким способом можно получить диапазон значений [math] [-2^{n-1}+1; 2^{n-1} - 1] [/math].

Достоинства:

• Простое получение кода отрицательных чисел

Недостатки метода:

• выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора

• существуют два нуля [math] +0 [/math] и [math] -0 [/math].

Дополнительный код (дополнение до двух)

Нумерация двоичных чисел в представлении c дополнением до двух.

Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two's complement).

Алгоритм получения дополнительного кода числа:

• если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число;
• если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.

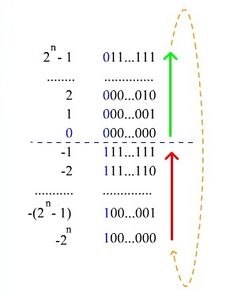
В качестве примера переведём число [math] -5 [/math] в дополнительный восьмибитный код. Прямой код модуля [math] -5 [/math] — [math] 0000101 [/math], обратный — [math] 1111010 [/math], прибавляем [math] 1 [/math], получаем [math] 1111011 [/math], приписываем [math] 1 [/math] в качестве знакового разряда, в результате получаем [math] 11111011 [/math].

Также дополнительный код отрицательного числа [math] A [/math], хранящегося в [math] n [/math] битах, равен [math] 2^n - |A| [/math]. По сути, дополнительный код представляет собой дополнение [math] |A| [/math] до [math] 0 [/math]: так как в [math] n [/math]-разрядной арифметике [math] 2^{n} = 0 [/math] (двоичная запись этого числа состоит из единицы и [math] n [/math] нулей, а в [math] n [/math]-разрядную ячейку помещаются только [math] n [/math] младших разрядов, то есть [math] n [/math] нулей), то верно равенство [math] 2^n - |A| + |A| = 0 [/math].

Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен [math] 2^n [/math]. Переведём [math] 11111011 [/math] обратно. Инвертируем — [math] 00000100 [/math], прибавляем [math] 1 [/math], получаем [math] 00000101 [/math] — модуль исходного числа [math] -5 [/math]. Проверим: [math] 11111011 + 00000101 = 100000000 [/math].

Можно получить диапазон значений [math] [-2^{n-1}; 2^{n-1} - 1] [/math].

Достоинства метода:

• возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие;
• нет проблемы двух нулей.

Недостатки:

• ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.

Литература

• Эндрю Таненбаум «Архитектура компьютера», 5-е изд., стр. 739—741

Ссылки

• Википедия — Дополнительный код (представление числа)

• Википедия — Прямой код

• Wikipedia — Signedness