Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора

Основные определения

Определение:

Контекстно-свободной грамматикой (англ. сontext-free grammar) называется грамматика, у которой в левых частях всех правил стоят только одиночные нетерминалы.

Определение:

Контекстно-свободный язык (англ. context-free language) — язык, задаваемый контекстно-свободной грамматикой.

Лево- и правосторонний вывод слова

Определение:

Выводом слова (англ. derivation of a word) [math]\alpha[/math] называется последовательность строк, состоящих из терминалов и нетерминалов. Первая строка последовательности состоит из одного стартового нетерминала. Каждая последующая строка получена из предыдущей путем замены любого нетерминала по одному (любому) из правил, а последней строкой в последовательности является слово [math]\alpha[/math].

Пример:

Рассмотрим грамматику, выводящую все правильные скобочные последовательности.

[math]"("[/math] и [math]")"[/math] — терминальные символы;

[math]S[/math] — стартовый нетерминал;

Правила:
[math]S\rightarrow (S)S[/math]
[math]S\rightarrow S(S)[/math]
[math]S\rightarrow \varepsilon[/math]
Выведем слово [math]"(()(()))()"[/math]:
[math]\boldsymbol{S}\Rightarrow (S)\boldsymbol{S} \Rightarrow (S)(\boldsymbol{S})S\Rightarrow(S)()\boldsymbol{S}\Rightarrow(\boldsymbol{S})()\Rightarrow(\boldsymbol{S}(S))()\Rightarrow(S(S)(\boldsymbol{S}))()\Rightarrow(S(S)(\boldsymbol{S}(S)))()\Rightarrow (S(\boldsymbol{S})((S)))()\Rightarrow(\boldsymbol{S}()((S)))()\Rightarrow(()((\boldsymbol{S})))()\Rightarrow(()(()))()[/math]

Определение:

Левосторонний вывод слова (англ. leftmost derivation)[math]\alpha[/math] — вывод, где каждая последующая строка получена из предыдущей путем замены по одному из правил самого левого встречающегося в строке нетерминала.

Определение:

Правосторонним выводом слова (англ. rightmost derivation) [math]\alpha[/math] — вывод, где каждая последующая строка получена из предыдущей путем замены по одному из правил самого правого встречающегося в строке нетерминала.

Рассмотрим левосторонний вывод скобочной последовательности из примера:
[math]\boldsymbol{S}\Rightarrow (\boldsymbol{S})S \Rightarrow ((\boldsymbol{S})S)S\Rightarrow (()\boldsymbol{S})S\Rightarrow(()\boldsymbol{S}(S))S\Rightarrow(()(\boldsymbol{S}))S\Rightarrow(()(\boldsymbol{S}(S)))S\Rightarrow(()((\boldsymbol{S})))S\Rightarrow(()(()))\boldsymbol{S}\Rightarrow(()(()))(\boldsymbol{S})S\Rightarrow(()(()))()\boldsymbol{S}\Rightarrow(()(()))()[/math]

Дерево разбора

Определение:

Деревом разбора грамматики (англ. parse tree) называется дерево, в вершинах которого записаны терминалы или нетерминалы. Все вершины, помеченные терминалами, являются листьями. Все вершины, помеченные нетерминалами, имеют детей. Дети вершины, в которой записан нетерминал, соответствуют раскрытию нетерминала по одному любому правилу (в левой части которого стоит этот нетерминал) и упорядочены так же, как в правой части этого правила.

Определение:

Крона дерева разбора — множество терминальных символов, упорядоченное в соответствии с номерами их достижения при обходе дерева в глубину из корня. Крона дерева разбора представляет из себя слово языка, которое выводит это дерево.

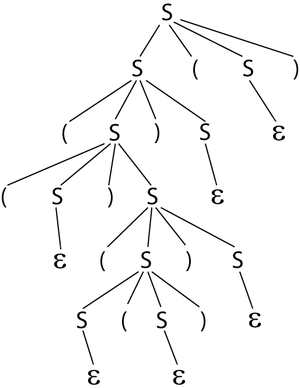
Построим дерево разбора скобочной последовательности из примера.

Однозначные грамматики

Определение:

Грамматика называется однозначной (англ. unambiguous grammar), если у каждого слова имеется не более одного дерева разбора в этой грамматике.

Лемма:

Пусть [math]\Gamma[/math] — однозначная грамматика. Тогда [math]\forall \omega \in \mathbb{L}(\Gamma)[/math] существует ровно один левосторонний (правосторонний) вывод.

Доказательство:

[math]\triangleright[/math]

Очевидно, что по дереву разбора однозначно восстанавливается левосторонний(правосторонний) вывод. Поскольку каждое слово из языка выводится только одним деревом разбора, то существует только один левосторонний(правосторонний) вывод этого слова.

[math]\triangleleft[/math]

Утверждение:

Грамматика из примера не является однозначной.

[math]\triangleright[/math]

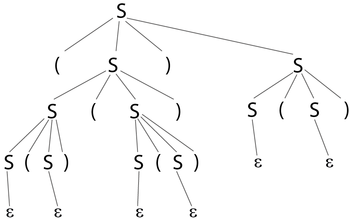
Выше уже было построено дерево разбора для слова [math]"(()(()))()"[/math]. Построим еще одно дерево разбора для данного слова. Например, оно будет выглядеть так: Таким образом, существует слово, у которого есть более одного дерева разбора в данной грамматике [math]\Rightarrow[/math] эта грамматика не является однозначной.

[math]\triangleleft[/math]

Утверждение:

Существуют языки, которые можно задать одновременно как однозначными, так и неоднозначными грамматиками.

[math]\triangleright[/math]

Для доказательства достаточно привести однозначную грамматику для языка правильных скобочных последовательностей (неоднозначной грамматикой для данного языка является грамматика из примера выше). Рассмотрим грамматику: [math]"("[/math] и [math]")"[/math] — терминальные символы; [math]S[/math] — стартовый нетерминал; Правила: 1) [math]S\rightarrow (S)S[/math] 2) [math]S\rightarrow \varepsilon[/math] Покажем, что эта грамматика однозначна. Для этого, используя индукцию, докажем, что для любого слова [math]\omega[/math], являющегося правильной скобочной последовательностью, в данной грамматике существует только одно дерево разбора. База: Если [math]\omega=\varepsilon[/math], то оно выводится только по второму правилу [math]\Rightarrow[/math] для него существует единственное дерево разбора. Переход: Пусть [math]\left\vert \omega \right\vert=n[/math] и [math]\forall \upsilon[/math]: [math]\left\vert \upsilon \right\vert \lt n[/math] и [math]\upsilon[/math] — правильная скобочная последовательность [math]\exists![/math] дерево разбора. Найдем в слове [math]\omega[/math] минимальный индекс [math]i \neq 0[/math] такой, что слово [math]\omega[0..i][/math] является правильной скобочной последовательностью. Так как [math]i \neq 0[/math] минимальный, то [math]\omega[0..i]=(\alpha)[/math]. Из того, что [math]\omega[/math] является правильной скобочной последовательностью [math]\Rightarrow[/math] [math]\alpha[/math] и [math]\beta=\omega[i+1..n-1][/math] — правильные скобочные последовательности, при этом [math]\left\vert \alpha \right\vert\lt n[/math] и [math]\left\vert \beta \right\vert\lt n \Rightarrow[/math] по индукционному предположению предположению у [math]\alpha[/math] и [math]\beta[/math] существуют единственные деревья разбора. Если мы покажем, что из части [math](S)[/math] первого правила можно вывести только слово [math](\alpha)[/math], то утверждение будет доказано (так как из первой части первого правила выводится [math]\alpha[/math], а из второй только [math]\beta[/math] и каждое из них по предположению выводится однозначно). Пусть из [math](S)[/math] была выведена часть слова [math]\omega[0..j]=(\gamma)[/math], где [math]j \lt i[/math], при этом [math]\gamma[/math] является правильной скобочной последовательностью, но тогда как минимальный индекс мы должны были выбрать [math]j[/math], а не [math]i[/math] — противоречие. Аналогично из [math](S)[/math] не может быть выведена часть слова [math]\omega[0..j][/math], где [math]j \gt i[/math], потому что тогда [math]\alpha[/math] не будет правильной скобочной последовательностью, так как в позиции [math]i[/math] баланс скобок будет отрицательный. Значит, из [math](S)[/math] была выведена часть слова [math]\omega[0..i] \Rightarrow \omega[/math] имеет единственное дерево разбора [math]\Rightarrow[/math] данная грамматика однозначная. Таким образом, для языка правильных скобочных последовательностей мы привели пример как однозначной, так и неоднозначной грамматики.

[math]\triangleleft[/math]

Однако, есть КС-языки, для которых не существует однозначных КС-грамматик. Такие языки и грамматики их порождающие называют существенно неоднозначными.

См. также

• Формальные грамматики
• Иерархия Хомского формальных грамматик
• Замкнутость КС-языков относительно различных операций
• Существенно неоднозначные языки

Литература

• Wikipedia — Context-free grammar
• Википедия — Контекстно-свободная грамматика
• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)