Теорема Понтрягина-Куратовского — различия между версиями
м (Добавлены категории, замена некоторых дефисов длинными тире) |
|||
| Строка 1: | Строка 1: | ||
| + | __TOC__ | ||
| + | |||
{{Теорема | {{Теорема | ||
|statement = | |statement = | ||
| Строка 6: | Строка 8: | ||
Необходимость условия очевидна. | Необходимость условия очевидна. | ||
=== Достаточность === | === Достаточность === | ||
| − | От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. Пусть <tex> G </tex> | + | От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных <tex> K_{5} </tex> или <tex> K_{3, 3} </tex>. Пусть <tex> G </tex> — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. |
==== G связен ==== | ==== G связен ==== | ||
Если <tex> G </tex> не связен, то его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. | Если <tex> G </tex> не связен, то его компоненты связности планарны и, следовательно, сам граф <tex> G </tex> планарен. | ||
| − | ==== G | + | ==== G — обыкновенный граф ==== |
В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. Тогда граф <tex> G - e </tex> планарен. Добавляя ребро <tex> e </tex> к графу <tex> G - e </tex> получим, что граф <tex> G </tex> он планарен. | В самом деле, пусть в графе <tex> G </tex> есть петля или кратное ребро <tex> e </tex>. Тогда граф <tex> G - e </tex> планарен. Добавляя ребро <tex> e </tex> к графу <tex> G - e </tex> получим, что граф <tex> G </tex> он планарен. | ||
| − | ==== G | + | ==== G — блок ==== |
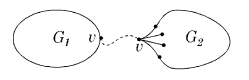
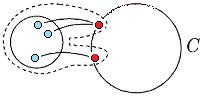
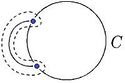
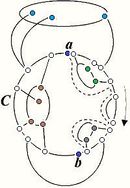
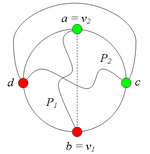
Пусть, от противного, в графе есть точка сочленения <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через | Пусть, от противного, в графе есть точка сочленения <tex> v </tex>. Через <tex> G_1 </tex> обозначим подграф графа <tex> G </tex>, порождённый вершинами одной из компонент связности графа <tex> G - v</tex> и вершинной <tex> v </tex>, а через | ||
<tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. (рис. 1) | <tex> G_2 </tex> подграф графа <tex> G </tex>, порождённый вершинами остальных компонент связности графа <tex> G - v </tex> и вершиной <tex> v </tex>. (рис. 1) | ||
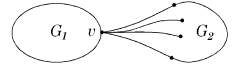
| Строка 21: | Строка 23: | ||
Таким образом мы получили укладку графа <tex> G </tex> на плоскости, что невозможно. | Таким образом мы получили укладку графа <tex> G </tex> на плоскости, что невозможно. | ||
<br/> <br/> | <br/> <br/> | ||
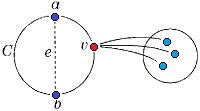
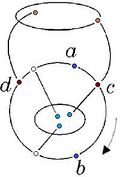
| − | Пусть <tex> e = ab </tex> | + | Пусть <tex> e = ab </tex> — произвольное ребро графа <tex> G </tex>, <tex> G' = G - e </tex>. |
# граф <tex> G' </tex> планарен в силу минимальности графа <tex> G </tex>. | # граф <tex> G' </tex> планарен в силу минимальности графа <tex> G </tex>. | ||
# граф <tex> G' </tex> связен в силу отсутствия в графе <tex> G </tex> мостов. | # граф <tex> G' </tex> связен в силу отсутствия в графе <tex> G </tex> мостов. | ||
| Строка 29: | Строка 31: | ||
# Если <tex> |VB| >= 3 </tex>, то существует цикл графа G', содержащий вершины <tex> a </tex> и <tex> b </tex>. | # Если <tex> |VB| >= 3 </tex>, то существует цикл графа G', содержащий вершины <tex> a </tex> и <tex> b </tex>. | ||
# Если <tex> |VB| = 2 </tex>, то в <tex> B </tex> имеется ребро <tex> e' = ab </tex>, но тогда в <tex> G </tex> имеются кратные рёбра <tex> e </tex> и <tex> e' </tex>, что невозможно. | # Если <tex> |VB| = 2 </tex>, то в <tex> B </tex> имеется ребро <tex> e' = ab </tex>, но тогда в <tex> G </tex> имеются кратные рёбра <tex> e </tex> и <tex> e' </tex>, что невозможно. | ||
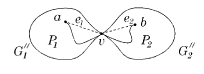
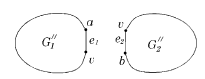
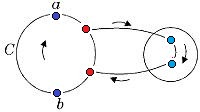
| − | # Если вершины <tex> a </tex> и <tex> b </tex> лежат в разных блоках графа <tex> G' </tex>, что существует точка сочленения <tex> v </tex>, принадлежащая любой простой (a, b)-цепи графа <tex> G' </tex>. Через <tex> G'_1 </tex> обозначим подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами компоненты связности графа <tex> G' - v </tex>, содержащей <tex> a </tex>, а через <tex> G'_2 </tex> - подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами остальных компонент связности графа <tEx> G' - v </tex> (в этом множестве лежит вершина <tex> b </tex>). Пусть <tex> G''_1 = G'_1 + e_1 </tex>, где <tex> e_1 = vb </tex> | + | # Если вершины <tex> a </tex> и <tex> b </tex> лежат в разных блоках графа <tex> G' </tex>, что существует точка сочленения <tex> v </tex>, принадлежащая любой простой (a, b)-цепи графа <tex> G' </tex>. Через <tex> G'_1 </tex> обозначим подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами компоненты связности графа <tex> G' - v </tex>, содержащей <tex> a </tex>, а через <tex> G'_2 </tex> - подграф графа <tex> G' </tex>, порождённый вершиной <tex> v </tex> и вершинами остальных компонент связности графа <tEx> G' - v </tex> (в этом множестве лежит вершина <tex> b </tex>). Пусть <tex> G''_1 = G'_1 + e_1 </tex>, где <tex> e_1 = vb </tex> — новое ребро (рис. 4) |
[[Файл:p-k.4.png|thumb|right|рис. 4]] | [[Файл:p-k.4.png|thumb|right|рис. 4]] | ||
Заметим, что в графе <tex> G''_1 </tex> рёбер меньше, чем в графе <tex> G </tex>. Действительно, вместо ребра <tex> e </tex> в <tex> G''_1 </tex> есть ребро <tex> e_1 </tex> и часть рёбер из графа <tex> G </tex> осталась в графе <tex> G''_2 </tex>. Аналогично, в графе <tex> G''_2 </tex> рёбер меньше, чем в графе <tex> G </tex>. <br/> | Заметим, что в графе <tex> G''_1 </tex> рёбер меньше, чем в графе <tex> G </tex>. Действительно, вместо ребра <tex> e </tex> в <tex> G''_1 </tex> есть ребро <tex> e_1 </tex> и часть рёбер из графа <tex> G </tex> осталась в графе <tex> G''_2 </tex>. Аналогично, в графе <tex> G''_2 </tex> рёбер меньше, чем в графе <tex> G </tex>. <br/> | ||
| Строка 72: | Строка 74: | ||
{{Лемма | {{Лемма | ||
|statement = | |statement = | ||
| − | 1) Любая внешняя часть встречает цикл <tex>C</tex> точно в двух точках, одна из которых лежит в <tex>C(a,b)</tex>, а другая | + | 1) Любая внешняя часть встречает цикл <tex>C</tex> точно в двух точках, одна из которых лежит в <tex>C(a,b)</tex>, а другая — в <tex>C(b,a)</tex>. |
|proof = | |proof = | ||
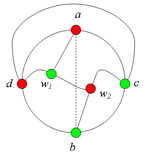
Если внешняя часть встречает цикл <tex>C</tex> точно в одной точке <tex>v</tex>, то <tex>v</tex> является точкой сочленения графа <tex>G</tex>, что невозможно (см. рис. 9). | Если внешняя часть встречает цикл <tex>C</tex> точно в одной точке <tex>v</tex>, то <tex>v</tex> является точкой сочленения графа <tex>G</tex>, что невозможно (см. рис. 9). | ||
| Строка 93: | Строка 95: | ||
{{Лемма | {{Лемма | ||
|statement = | |statement = | ||
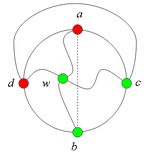
| − | 3) Существует внешняя часть, встречающая <tex>C(a,b)</tex> в точке <tex>c</tex> и <tex>C(b,a)</tex> | + | 3) Существует внешняя часть, встречающая <tex>C(a,b)</tex> в точке <tex>c</tex> и <tex>C(b,a)</tex> — в точке <tex>d</tex>, для которой найдётся внутренняя часть, являющаяся одновременно <tex>(a,b)</tex>-разделяющей и <tex>(c,d)</tex>-разделяющей (см. рис. 12). |
[[Файл:pict-6.jpg|center|120px|рис. 12]] | [[Файл:pict-6.jpg|center|120px|рис. 12]] | ||
|proof = | |proof = | ||
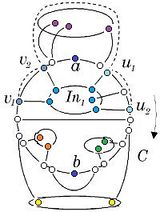
| − | Пусть, от противного, лемма 3 неверна. Упорядочим <tex>(a,b)</tex>-разделяющие внутренние части в порядке их прикрепления к циклу <tex>C</tex> при движении по циклу от <tex>a</tex> до <tex>b</tex> и обозначим их соответственно через <tex>In_{1},In_{2},...</tex>. Пусть <tex>u_{1}</tex> и <tex>u_{2}</tex> | + | Пусть, от противного, лемма 3 неверна. Упорядочим <tex>(a,b)</tex>-разделяющие внутренние части в порядке их прикрепления к циклу <tex>C</tex> при движении по циклу от <tex>a</tex> до <tex>b</tex> и обозначим их соответственно через <tex>In_{1},In_{2},...</tex>. Пусть <tex>u_{1}</tex> и <tex>u_{2}</tex> — первая и последняя вершины из <tex>C(a,b)</tex>, в которых <tex>In_{1}</tex> встречает цикл <tex>C</tex>, а <tex>v_{1}</tex> и <tex>v_{2}</tex> — первая и последняя вершины из <tex>C(b,a)</tex>, в которых <tex>In_{1}</tex> встречает цикл <tex>C</tex> (возможно, вообще говоря, <tex>u_{1} = u_{2}</tex> или <tex>v_{1} = v_{2}</tex>). Поскольку лемма 3 неверна, для любой внешней части обе её вершины, в которых она встречает <tex>C</tex>, лежат либо на <tex>C[v_{2},u_{1}]</tex>, либо на <tex>C[u_{2},v_{1}]</tex>. Тогда снаружи цикла <tex>C</tex> можно провести жорданову кривую <tex>P</tex>, не пересекая рёбер графа <tex>G'</tex>, соединяющую <tex>v_{2}</tex> с <tex>u_{1}</tex> (см. рис. 13). |
[[Файл:pict-7.jpg|center|160px|рис. 13]] | [[Файл:pict-7.jpg|center|160px|рис. 13]] | ||
Поскольку на участках <tex>C(u_{1},u_{2})</tex> и <tex>C(v_{1},v_{2})</tex> нет точек прикрепления внешних частей, используя жорданову кривую <tex>P</tex>, внутреннюю часть <tex>In_{1}</tex> можно перебросить ("вывернуть" наружу от цикла <tex>C</tex>) во внешнюю область цикла <tex>C</tex>, т.е. уложить её снаружи от цикла <tex>C</tex> и сделать её внешней частью. | Поскольку на участках <tex>C(u_{1},u_{2})</tex> и <tex>C(v_{1},v_{2})</tex> нет точек прикрепления внешних частей, используя жорданову кривую <tex>P</tex>, внутреннюю часть <tex>In_{1}</tex> можно перебросить ("вывернуть" наружу от цикла <tex>C</tex>) во внешнюю область цикла <tex>C</tex>, т.е. уложить её снаружи от цикла <tex>C</tex> и сделать её внешней частью. | ||
| Строка 102: | Строка 104: | ||
}} | }} | ||
| − | |||
| − | + | == Разбор случаев взаимного положения ''a, b, c, d, u1, u2, v1, v2'' == | |
Рассмотрим 2 случая. | Рассмотрим 2 случая. | ||
[[Файл:Case_1.png|thumb|right|рис. 1]] | [[Файл:Case_1.png|thumb|right|рис. 1]] | ||
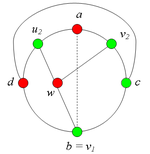
| Строка 123: | Строка 124: | ||
2.1.3. Пусть <tex>u_2</tex> лежит на <tex>C(b, d)</tex>.<br> | 2.1.3. Пусть <tex>u_2</tex> лежит на <tex>C(b, d)</tex>.<br> | ||
| − | Тогда в графе <tex>G</tex> есть подграф, гомеоморфный <tex> | + | Тогда в графе <tex>G</tex> есть подграф, гомеоморфный <tex>K_{3,3}</tex>(рис. 5).<br> |
<p> | <p> | ||
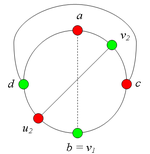
| Строка 151: | Строка 152: | ||
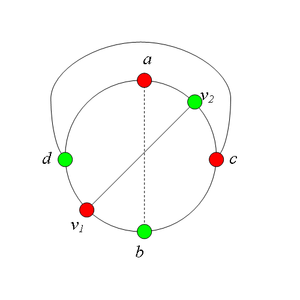
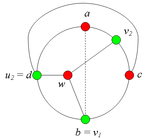
2.3. Пусть <tex>v_2 = a</tex>(рис. 9).<br> | 2.3. Пусть <tex>v_2 = a</tex>(рис. 9).<br> | ||
| − | Рассмотрим теперь пару вершин <tex>u_1</tex> и <tex>u_2</tex>. Будем считать, что <tex>u_1 = c</tex> и <tex>u_2 = d</tex>, поскольку все другие случаи расположения вершин <tex>u_1</tex> и <tex>u_2</tex> так же, как были рассмотрены все случаи расположения <tex>v_1</tex> и <tex>v_2</tex>. Пусть <tex>P_1</tex> и <tex>P_2</tex> | + | Рассмотрим теперь пару вершин <tex>u_1</tex> и <tex>u_2</tex>. Будем считать, что <tex>u_1 = c</tex> и <tex>u_2 = d</tex>, поскольку все другие случаи расположения вершин <tex>u_1</tex> и <tex>u_2</tex> так же, как были рассмотрены все случаи расположения <tex>v_1</tex> и <tex>v_2</tex>. Пусть <tex>P_1</tex> и <tex>P_2</tex> — соответственно кратчайшие простые <tex>(a, b)</tex>-цепь и <tex>(c, d)</tex>-цепь по внутренней части <tex>In</tex>(рис. 10). |
Заметим, что <tex>P_1</tex> и <tex>P_2</tex> имеют общую точку.<br> | Заметим, что <tex>P_1</tex> и <tex>P_2</tex> имеют общую точку.<br> | ||
| Строка 171: | Строка 172: | ||
==Литература== | ==Литература== | ||
| − | * Асанов М | + | * Асанов М., Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы |
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Укладки графов ]] | [[Категория: Укладки графов ]] | ||
Версия 09:49, 21 октября 2010
Содержание
| Теорема: | ||||||||||||||||||||||||||||||||
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных , и не содержит подграфов, гомеоморфных . | ||||||||||||||||||||||||||||||||
| Доказательство: | ||||||||||||||||||||||||||||||||
НеобходимостьНеобходимость условия очевидна. ДостаточностьОт противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных или . Пусть — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связенЕсли не связен, то его компоненты связности планарны и, следовательно, сам граф планарен. G — обыкновенный графВ самом деле, пусть в графе есть петля или кратное ребро . Тогда граф планарен. Добавляя ребро к графу получим, что граф он планарен. G — блокПусть, от противного, в графе есть точка сочленения . Через обозначим подграф графа , порождённый вершинами одной из компонент связности графа и вершинной , а через подграф графа , порождённый вершинами остальных компонент связности графа и вершиной . (рис. 1) Возьмём укладку графа на плоскости такую, что вершина лежит на границе верхней грани. Затем во внешней грани графа возьмём укладку графа такую, что вершина будет представлена на плоскости в двух экземплярах. (рис. 2) Соединим два экземпляра вершины пучком жордановых линий, не допуская лишних пересечений с укладками графов и , состоящим из такого количества линий, какова степень вершины в графе . Далее отбросим вхождение вершины в граф , заменяя инцидентные её рёбра на жордановы линии, полученные из линий указанного пучка и рёбер (рис. 3) Таким образом мы получили укладку графа на плоскости, что невозможно.
В G' существует цикл, содержащий вершины a и bПусть и лежат в одном блоке графа .
Заметим, что в графе рёбер меньше, чем в графе . Действительно, вместо ребра в есть ребро и часть рёбер из графа осталась в графе . Аналогично, в графе рёбер меньше, чем в графе . Отметим, что опять вершина представлена на плоскости в двух экземплярах. Очевидно, добавление ребра не меняет планарности графа . Склеим оба вхождения вершины точно так же, как это мы сделали в предыдущем пункте доказательства (рис. 6). Сотрем затем ранее добавленные ребра и . В результате мы получим укладку графа на плоскости, что невозможно. Утверждение доказано. Вспомогательные определения и утверждение об одновременно разделяющейся внутренней частиСреди всех укладок графа на плоскости и среди всех циклов , содержащих и , зафиксируем такую укладку и такой цикл, что внутри области, ограниченной циклом , лежит максимальное возможное число граней графа . Зафиксируем один из обходов по циклу (на рисунках будем рассматривать обход по часовой стрелке по циклу ). Для вершин и цикла через будем обозначать простую -цепь, идущую по циклу от до в направлении обхода цикла. Конечно, . Положим {}, т.е. получено из отбрасыванием вершин и .
В силу связности графа для любой внешней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
В силу связности графа для любой внутренней компоненты должны существовать рёбра в , соединяющие её с вершинами цикла .
Будем говорить, что внешняя (внутренняя) часть встречает цикл в своих точках прикрепления к циклу .
Аналогично можно ввести понятие -разделяющей внутренней части. Заметим, что внутрення часть может встречать цикл , вообще говоря, более чем в двух точках, но не менее чем в двух точках.
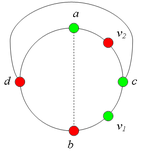
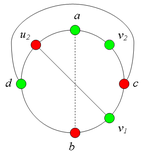
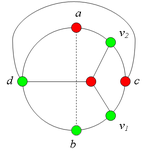
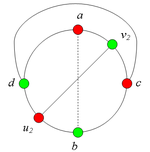
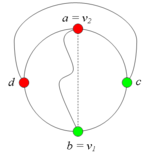
Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2Рассмотрим 2 случая. 1. Пусть пара вершин и является -разделяющей. 2. Пусть пара вершин и не является -разделяющей. 2.1. Пусть и лежат на , т.е. и (рис. 2). 2.1.1 Пусть лежит на . 2.1.2. Пусть . 2.1.3. Пусть лежит на . Теперь рассмотрим случаи, когда хотя бы одна из вершин и не лежит на . Без ограничения общности будем считать, что это вершина , т.е (поскольку лежит на ). 2.2. Пусть . 2.2.1. Пусть лежит на . 2.2.2. Пусть . 2.2.3. Пусть лежит на . 2.3. Пусть (рис. 9). 2.3.1. Пусть цепи и имеют более одной общей точки. 2.3.2. Пусть цепи и имеют точно одну общую точку . | ||||||||||||||||||||||||||||||||
Литература
- Асанов М., Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы