Построение по НКА эквивалентного ДКА, алгоритм Томпсона

Описание

Алгоритм Томпсона строит по НКА эквивалентный ДКА следующим образом:

• Начало.
• Шаг 1. Помещаем в очередь [math]Q[/math] множество, состоящее только из стартовой вершины.
• Шаг 2. Затем, пока очередь не пуста выполняем следующие действия:
  • Достаем из очереди множество, назовем его [math]q[/math]
  • Для каждого [math]c \in \Sigma[/math] построим множество, содержащее состояния, в которые ведет символ [math]c[/math] из каждого состояния из [math]q[/math]. Затем положим построенное множество в очередь [math]Q[/math] только если оно не лежало там раньше. Каждое такое множество в итоговом ДКА будет отдельной вершиной, в которую будут вести переходы по соответствующим символам.
  • Если в множестве [math]q[/math] хотя бы одна из вершин была терминальной в НКА, то соответствующая данному множеству вершина в ДКА также будет терминальной.
• Конец.

Построение эквивалентного ДКА по НКА

Пусть нам дан произвольный НКА: [math]\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to 2^Q \rangle[/math].

Построим по нему следующий ДКА: [math]\langle \Sigma , Q_d, s_d \in Q_d, T_d \subset Q_d, \delta_d : Q_d \times \Sigma \to Q_d \rangle[/math], где:

1. [math]Q_d = \{q_d \mid q_d \subset 2^Q \}[/math],
2. [math]s_d = \{s\}[/math],
3. [math]T_d = \{q \in Q_d \mid \exists p \in T : p \in q\}[/math],
4. [math]\delta_d(q, c) = \{ \delta(a, c) \mid a \in q \}[/math].

Доказательство эквивалентности

Теорема:

Построенный ДКА эквивалентен данному НКА.

Доказательство:

[math]\triangleright[/math]

Докажем, что любое слово, которое принимает НКА, будет принято построенным ДКА. Заметим, что [math]\forall q \in q_d, \forall c \in \Sigma, \forall p \in \delta(q, c): p \in \delta_d(q_d, c)[/math]. Рассмотрим слово [math]w=w_1 \dots w_m[/math], которое принимает автомат НКА: [math]\langle s, w_1w_2 \dots w_m \rangle \vdash \langle u_1, w_2 \dots w_m \rangle \vdash \langle u_m, \varepsilon \rangle, u_m \in T[/math]. Проверим, что построенный ДКА тоже принимает это слово. Заметим, что [math]s \in s_d[/math], а, значит, исходя из нашего наблюдения, мы получаем, что [math]u_1 \in {u_d}_1[/math], где [math]{u_d}_1 = \delta_d(s, w_1)[/math]. Далее, несложно заметить, что [math]\forall i \leqslant m : u_i \in {u_d}_i[/math], где [math]\langle s_d, w_1w_2 \dots w_m \rangle \vdash \langle {u_d}_1, w_2 \dots w_m \rangle \vdash \langle {u_d}_i, w_{i + 1} \dots w_m\rangle[/math]. Таким образом, [math]u_m \in {u_d}_m[/math], а из определения терминальных состояний в построенном ДКА мы получаем, что [math]{u_d}_m \in T_d[/math], то есть наш ДКА тоже принимает cлово [math]w[/math]. Докажем, что любое слово, которое принимает построенный ДКА, принимает и НКА. Сначала сделаем наблюдение, что если [math]q_d=\{q\}[/math], и мы из него достигли по строке [math]S[/math] какого-то состояния [math]p_d[/math], то [math]\forall p \in p_d[/math] существует путь из [math]q[/math] в [math]p[/math] в НКА по строке [math]S[/math]. Рассмотрим слово [math]w=w_1 \dots w_m[/math], которое принимает автомат ДКА: [math]\langle s_d, w_1w_2 \dots w_m \rangle \vdash \langle {u_d}_1, w_2 \dots w_m \rangle \vdash \langle {u_d}_m, \varepsilon \rangle, {u_d}_m \in T_d[/math]. Проверим, что НКА тоже принимает это слово. Так как [math]s_d = \{s\}[/math], и мы из [math]s_d[/math] достигли [math]{u_d}_m \in T_d[/math], возьмём любое терминальное состояние [math]u_m \in {u_d}_m[/math]. По нашему наблюдению в НКА есть путь из [math]s[/math] в [math]u_m[/math] по строке [math]w[/math], а, значит, НКА принимает это слово. Таким образом, множества слов, допускаемых ДКА и НКА, совпадают, то есть они эквивалентны.

[math]\triangleleft[/math]

Алгоритм Томпсона

Данный алгоритм преобразовывает НКА в эквивалентный ДКА. Будем использовать вышеуказанный способ построения с одним дополнением — не будем учитывать состояния недостижимые из стартового. Поэтому в алгоритме используется обход в ширину.

Алгоритм

[math]P[/math] — очередь состояний, соответствующих множествам, состоящих из состояний НКА. [math]Q[/math] — массив множеств, соответствующих состояниям ДКА. [math]s[/math] — стартовое состояние НКА.

Automaton getDFAbyNFA([math]\langle \Sigma, Q_0, s, T_0, \delta_0 \rangle[/math] : Automaton):
   [math]P[/math].push({s})
   [math]Q[/math] = [math]\varnothing[/math]
   while ([math]P[/math] [math] \neq [/math] [math]\varnothing [/math])
      [math]P[/math].pop([math]p_d[/math])
      for ([math]c[/math] in [math]\Sigma[/math])
         [math]q_d[/math] = [math]\varnothing[/math]
         for ([math]p[/math] in [math]p_d[/math]) 
            [math]q_d[/math] = [math]q_d \cup \{ \delta_0(p, c) \}[/math]
         if ([math]q_d[/math] not in [math]Q[/math])
            [math]P[/math].push([math]q_d[/math])
            [math]Q[/math].add([math]q_d[/math])   
            [math]\delta(p_d, q_d)[/math] = [math]c[/math]
   for ([math]q[/math] in [math]Q[/math])
      if ([math]\exists q_d[/math] in [math]q: q_d[/math] in [math]T_0[/math])
        [math]T[/math].add[math](q)[/math]
   return [math]\langle \Sigma, Q, \{s\}, T, \delta \rangle[/math]

Асимптотика

Так как количество подмножеств множества состояний НКА не более, чем [math]2^n[/math], а каждое подмножество мы обрабатываем ровно один раз за время [math]O(n)[/math], получаем верхнюю оценку времени работы алгоритма — [math]O(n \cdot 2^n)[/math].

Пример

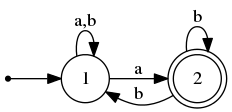
Пусть нам дан недетерминированный конечный автомат:

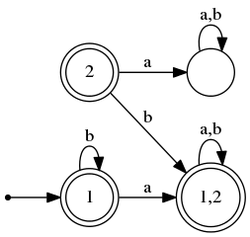
По нашему заданию эквивалентного ДКА мы получаем:

1. Помещаем в очередь множество из одной стартовой вершины — [math]\{1\}[/math]: [math]Q = \{\{1\}\}[/math].
2. Достаём из очереди множество [math]\{1\}[/math]: [math]Q = \{\}[/math].
3. [math]q_d(\{1\}, a) = \{1, 2\}[/math], кладём множество [math]\{1, 2\}[/math] в очередь: [math]Q = \{\{1, 2\}\}[/math].
4. [math]q_d(\{1\}, b) = \{1\}[/math], нам не надо класть множество [math]\{1\}[/math] в очередь, так как оно уже там было.
5. Достаём из очереди множество [math]\{1, 2\}[/math]: [math]Q = \{\}[/math].
6. [math]q_d(\{1, 2\}, a) = \{1, 2\}[/math], нам не надо класть множество [math]\{1, 2\}[/math] в очередь, так как оно уже там было.
7. [math]q_d(\{1, 2\}, b) = \{1, 2\}[/math], нам не надо класть множество [math]\{1, 2\}[/math] в очередь, так как оно уже там было.
8. Помечаем все терминальные вершины, в данном случае — [math]\{1, 2\}[/math].

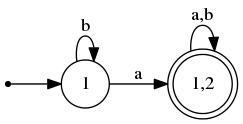
В итоге получаем ДКА, эквивалентный исходному:

.

См. также

• Регулярные языки: два определения и их эквивалентность
• Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний
• Теорема Клини (совпадение классов автоматных и регулярных языков)

Источники информации

• Серебряков В.А. Теория и реализация языков программирования. М.: МЗ-Пресс, 2003 (1-е изд.) и 2006 (2-е изд) — С. 294. — ISBN 5-94073-094-9