Пересечение прямоугольника с множеством непересекающихся отрезков (segment tree) — различия между версиями
(→Построение дерева) |
(Уточнение в формулировке) |
||
| Строка 10: | Строка 10: | ||
Построим сбалансированное бинарное дерево, листам которого будут соответствовать элементарные интервалы, а внутренним вершинам — объединения интервалов в потомках. | Построим сбалансированное бинарное дерево, листам которого будут соответствовать элементарные интервалы, а внутренним вершинам — объединения интервалов в потомках. | ||
Будем обозначать интервал, соответствующий вершине <tex>v</tex>, <tex>Int(v)</tex>. | Будем обозначать интервал, соответствующий вершине <tex>v</tex>, <tex>Int(v)</tex>. | ||
| − | В каждой вершине будем хранить соответствующий ей интервал и множество отрезков <tex>I(v)</tex>, таких что <tex>I(v) \subset I</tex> и <tex>\forall [x : x'] \in I(v) : Int(v) \subset [x : x'], Int(parent(v)) \not\subset [x : x']</tex>. По-человечески это значит, что интервал вершины должен полностью лежать внутри отрезка и | + | В каждой вершине будем хранить соответствующий ей интервал и множество отрезков <tex>I(v)</tex>, таких что <tex>I(v) \subset I</tex> и <tex>\forall [x : x'] \in I(v) : Int(v) \subset [x : x'], Int(parent(v)) \not\subset [x : x']</tex>. По-человечески это значит, что интервал вершины должен полностью лежать внутри отрезка и для родителя вершины это не так. По картинке должно быть понятно. |
{{Лемма | {{Лемма | ||
Версия 20:21, 19 января 2015
Задача
Есть множество непересекающихся отрезков в , нужно уметь отвечать на запросы, какие из них пересекают границу данного axis-aligned (стороны параллельны осям координат) прямоугольника.
Дерево отрезков
Для решения задачи потребуется структура данных, которая называется дерево отрезков (segment tree). NB: по-русски этими словами принято обозначать несколько другую структуру данных, здесь не о ней.
Пусть — множество отрезков на вещественной оси. Возьмем концы этих отрезков и отсортируем их, получим точки . Назовем множеством элементарных интервалов .
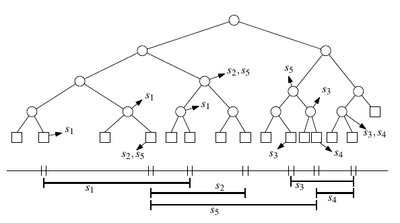
Построим сбалансированное бинарное дерево, листам которого будут соответствовать элементарные интервалы, а внутренним вершинам — объединения интервалов в потомках. Будем обозначать интервал, соответствующий вершине , . В каждой вершине будем хранить соответствующий ей интервал и множество отрезков , таких что и . По-человечески это значит, что интервал вершины должен полностью лежать внутри отрезка и для родителя вершины это не так. По картинке должно быть понятно.
| Лемма (Оценка на память): |
Дерево отрезков занимает памяти. |
| Доказательство: |
|
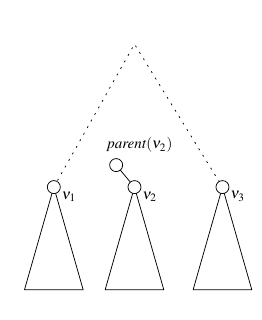
Всего элементарных интервалов не больше (в случае, когда все отрезки не пересекаются: для каждого отрезок левее , , , и еще один ). Так как дерево сбалансированное, его глубина . Утверждается, что один отрезок на одной глубине встречается не более двух раз. Пусть это не так, возьмем три упорядоченные вершины , содержащие этот отрезок. Очевидно, что сосед тоже содержит этот отрезок (см. картинку). Тогда этот отрезок должен содержаться в . Противоречие. Глубина , всего отрезков , на каждом уровне отрезок встречается раз — победа. |
Построение дерева
Сначала сортируем концы отрезков из за . За собираем сбалансированное дерево (просто поднимаясь от листьев к корню и объединяя интервалы). Осталось найти для вершин дерева. Для этого вставим туда каждый отрезок по такому алгоритму:
def InsertSegment(v, [x : x']): if : v.Add([x : x']) else: if : InsertSegment(v.Left, [x : x']) if : InsertSegment(v.Right, [x : x'])
Это работает за , потому что на каждом уровне есть не более двух вершин, в которые отрезок нужно вставить и еще не более двух вершин, содержащих его концы. Таким образом, на каждом уровне нужно обработать не более четырех вершин. Итого для всех отрезков получаем .
Запрос
Теперь научимся отвечать на запрос, какие отрезки содержат заданную точку.
def Query(v, p, S): S = S I(v) if !v.IsLeaf: if : Query(v.Left, p) else Query(v.Right, p) Query(root, p, )
Запрос работает за , где — размер ответа.
Алгоритм
Чтобы решить исходную задачу, нужно уметь находить, какие отрезки из пересекают axis-aligned отрезок . Рассмотрим случай, когда параллелен оси , для все делается аналогично.
В дереве отрезков будем хранить их проекции на ось . Это позволит найти, какие отрезки пересекают бесконечную вертикальную линию. Осталось найти, какие из них пересекают заданный отрезок.
Используем то, что отрезки не пересекаются, и : это значит, что отрезки внутри элементарного интервала могут быть вертикально упорядочены. В вместо списка теперь будем хранить дерево поиска.
При запросе будем выдавать только те отрезки, для которых верхняя граница запроса выше точки пересечения с вертикальной линией, а нижняя — ниже (то есть все, что находится между lower_bound и upper_bound в дереве, проверяем выше/ниже поворотом).
Таким образом, обработка одной вершины занимает времени, где — количество отрезков в ответе, полученных из вершины , всего посещенных вершин , итого . Препроцессинг выполняется за из-за вставки в дерево поиска.
Ссылки
- Английская википедия
- de Berg, van Kreveld, Overmars, Schwarzkopf "Computational Geometry Algorithms and Applications", p. 231