МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность — различия между версиями
Lidia2008 (обсуждение | вклад) (Новая страница: «== Допустимость по заключительному состоянию == <font face="Times" size="3"> *'''Определение: '''Пусть <tex>\…») |
Lidia2008 (обсуждение | вклад) (→Эквивалентность автоматов) |
||
| Строка 19: | Строка 19: | ||
[[Файл:EqualStackAutomata.png|left]] | [[Файл:EqualStackAutomata.png|left]] | ||
| − | '''1.''' Добавим переходы по <tex>\varepsilon</tex> из каждого допускающего состояния автомата <tex>\mathcal{P}_{T}</tex> в новое состояние <tex>p</tex>, которое отвечает за очистку стека. Находясь в состоянии <tex>p</tex>, автомат <tex>\mathcal{P_{N}}</tex> опустошает свой магазин и ничего не прочитывает на входе. Таким образом, как только исходный автомат <tex>\mathcal{P}_{T}</tex> приходит в допускающее состояние, прочитав слово <tex>w</tex>, <tex>\mathcal{P_{N}}</tex> опустошает свой магазин, также прочитав | + | '''1.''' Добавим переходы по <tex>\varepsilon</tex> из каждого допускающего состояния автомата <tex>\mathcal{P}_{T}</tex> в новое состояние <tex>p</tex>, которое отвечает за очистку стека. Находясь в состоянии <tex>p</tex>, автомат <tex>\mathcal{P_{N}}</tex> опустошает свой магазин и ничего не прочитывает на входе. Таким образом, как только исходный автомат <tex>\mathcal{P}_{T}</tex> приходит в допускающее состояние, прочитав слово <tex>w</tex>, <tex>\mathcal{P_{N}}</tex> опустошает свой магазин, также прочитав слово <tex>w</tex>. |
| + | |||
| + | '''2.''' Во избежание случая, когда <tex>\mathcal{P}_{T}</tex> может опустошить свой магазин без допуска, <tex>\mathcal{P_{N}}</tex> использует свой маркер дна <tex>Z_{1}</tex>. Добавление нового стартового состояния <tex>s</tex> позволяет затолкнуть маркер <tex>Z_{0}</tex> автомата <tex>\mathcal{P}_{T}</tex> в магазин и перейти в стартовое состояние <tex>\mathcal{P}_{T}</tex>. | ||
| + | |||
| + | '''3.''' Каждый переход <tex>\mathcal{P}_{T}</tex> есть и у автомата <tex>\mathcal{P_{N}}</tex>, символ <tex>Z_{1}</tex> хранится в магазине под всеми символами из <tex>\Gamma</tex> и является символом, по которому нет переходов в <tex>\mathcal{P}_{T}</tex>. Тогда <tex>\mathcal{P_{N}}</tex> может совершить следующие действия: <tex>(s, w, Z_{1})\vdash (s_{0}, w, Z_{0} Z_{1})\vdash (q, \varepsilon, \alpha Z_{1})\vdash (p, \varepsilon,\varepsilon) </tex>, что означает <tex>\mathcal{P_{N}}</tex> допускает слово <tex>w</tex> по пустому магазину. | ||
| + | |||
| + | |||
| + | |||
| − | |||
</font> | </font> | ||
| + | <font face="Times" size="3"> | ||
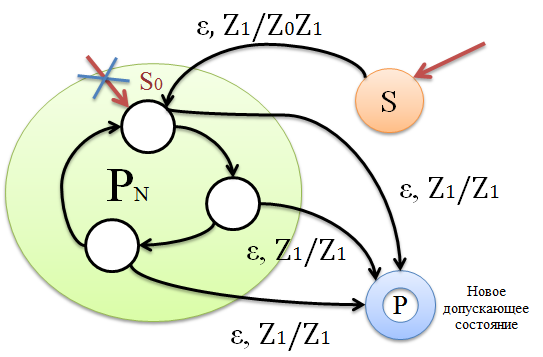
| + | *'''Доказательство:'''<tex>\Leftarrow</tex> Исходя из МП-автомата <tex>\mathcal{P}_{T}</tex>, допускающего язык <tex>L</tex> по пустому стеку, построим МП-автомат <tex>\mathcal{P_{N}}</tex>, допускающий <tex>L</tex> по заключительному состоянию. | ||
| + | [[Файл:EqualAllowAutomataPict.png|left]] | ||
Версия 01:07, 28 октября 2010
Допустимость по заключительному состоянию
- Определение: Пусть - МП-автомат. Тогда языком, допускаемым автоматом по заключительному состоянию, является для некоторого состояния и произвольной магазинной цепочки . Начиная с стартовой вершины и с на входе, автомат прочитывает слово и достигает допускающего состояния. Содержимое магазина в этот момент не имеет значения.
Допустимость по пустому магазину
- Определение: Для МП-автомата определим множество допускающих слов как , где - произвольное состояние. Таким образом автомат прочитывает слово , полностью опустошив свой магазин. Множество заключительных состояний не имеет значение.
Эквивалентность автоматов
- Теорема: Классы языков, допускаемых МП-автоматами по заключительному состоянию и по пустому магазину (стеку), совпадают.
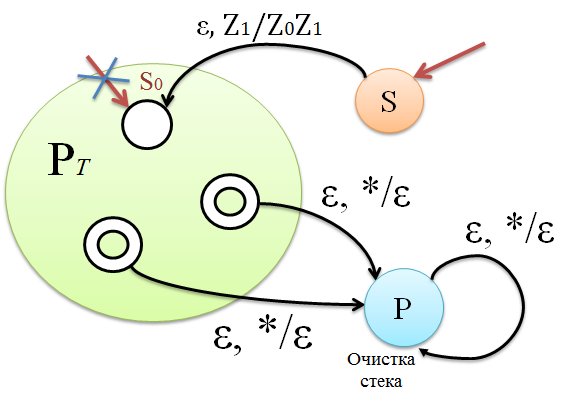
- Доказательство: Исходя из МП-автомата , допускающего язык по заключительному состоянию, построим другой МП-автомат , который допускает язык по пустому стеку.
1. Добавим переходы по из каждого допускающего состояния автомата в новое состояние , которое отвечает за очистку стека. Находясь в состоянии , автомат опустошает свой магазин и ничего не прочитывает на входе. Таким образом, как только исходный автомат приходит в допускающее состояние, прочитав слово , опустошает свой магазин, также прочитав слово .
2. Во избежание случая, когда может опустошить свой магазин без допуска, использует свой маркер дна . Добавление нового стартового состояния позволяет затолкнуть маркер автомата в магазин и перейти в стартовое состояние .
3. Каждый переход есть и у автомата , символ хранится в магазине под всеми символами из и является символом, по которому нет переходов в . Тогда может совершить следующие действия: , что означает допускает слово по пустому магазину.
- Доказательство: Исходя из МП-автомата , допускающего язык по пустому стеку, построим МП-автомат , допускающий по заключительному состоянию.