МП-автоматы, допуск по пустому стеку и по допускающему состоянию, эквивалентность — различия между версиями
Lidia2008 (обсуждение | вклад) (→Допуск по пустому магазину) |
Lidia2008 (обсуждение | вклад) (→Эквивалентность автоматов) |
||
| Строка 19: | Строка 19: | ||
<font face="Times" size="3"> | <font face="Times" size="3"> | ||
| − | + | {{Теорема | |
| − | + | |statement= Классы языков, допускаемых МП-автоматами по заключительному состоянию и по пустому магазину (стеку), совпадают. | |
| + | |proof= <tex>\Rightarrow</tex> Исходя из МП-автомата <tex>\mathcal{P}_{T}</tex>, допускающего язык <tex>L</tex> по заключительному состоянию, построим другой МП-автомат <tex>\mathcal{P_{N}}</tex>, который допускает язык <tex>L</tex> по пустому стеку. | ||
[[Файл:EqualStackAutomata.png|left]] | [[Файл:EqualStackAutomata.png|left]] | ||
| Строка 27: | Строка 28: | ||
'''2.''' Во избежание случая, когда <tex>\mathcal{P}_{T}</tex> может опустошить свой магазин без допуска, <tex>\mathcal{P_{N}}</tex> использует свой маркер дна <tex>Z_{1}</tex>. Добавление нового стартового состояния <tex>s</tex> позволяет затолкнуть маркер <tex>Z_{0}</tex> автомата <tex>\mathcal{P}_{T}</tex> в магазин и перейти в стартовое состояние <tex>\mathcal{P}_{T}</tex>. | '''2.''' Во избежание случая, когда <tex>\mathcal{P}_{T}</tex> может опустошить свой магазин без допуска, <tex>\mathcal{P_{N}}</tex> использует свой маркер дна <tex>Z_{1}</tex>. Добавление нового стартового состояния <tex>s</tex> позволяет затолкнуть маркер <tex>Z_{0}</tex> автомата <tex>\mathcal{P}_{T}</tex> в магазин и перейти в стартовое состояние <tex>\mathcal{P}_{T}</tex>. | ||
| − | '''3.''' Каждый переход <tex>\mathcal{P}_{T}</tex> есть и у автомата <tex>\mathcal{P_{N}}</tex>, символ <tex>Z_{1}</tex> хранится в магазине под всеми символами из <tex>\Gamma</tex> и является символом, по которому нет переходов в <tex>\mathcal{P}_{T}</tex>. Тогда <tex>\mathcal{P_{N}}</tex> может совершить следующие действия: <tex>(s, w, Z_{1})\vdash (s_{0}, w, Z_{0} Z_{1})\vdash^{*} (q, \varepsilon, \alpha Z_{1})\vdash^{*} (p, \varepsilon,\varepsilon) </tex>, что означает <tex>\mathcal{P_{N}}</tex> допускает слово <tex>w</tex> по пустому магазину. | + | '''3.''' Каждый переход <tex>\mathcal{P}_{T}</tex> есть и у автомата <tex>\mathcal{P_{N}}</tex>, символ <tex>Z_{1}</tex> хранится в магазине под всеми символами из <tex>\Gamma</tex> и является символом, по которому нет переходов в <tex>\mathcal{P}_{T}</tex>. Тогда <tex>\mathcal{P_{N}}</tex> может совершить следующие действия: <tex>(s, w, Z_{1})\vdash (s_{0}, w, Z_{0} Z_{1})\vdash^{*} (q, \varepsilon, \alpha Z_{1})\vdash^{*} (p, \varepsilon,\varepsilon) </tex>, что означает <tex>\mathcal{P_{N}}</tex> допускает слово <tex>w</tex> по пустому магазину. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <tex>\Leftarrow</tex> Исходя из МП-автомата <tex>\mathcal{P}_{T}</tex>, допускающего язык <tex>L</tex> по пустому стеку, построим МП-автомат <tex>\mathcal{P_{N}}</tex>, допускающий <tex>L</tex> по заключительному состоянию. | |
[[Файл:EqualAllowAutomataPict.png|left]] | [[Файл:EqualAllowAutomataPict.png|left]] | ||
| Строка 42: | Строка 43: | ||
'''2.''' Добавим новое допускающее состояние <tex>p</tex>, в которое автомат переходит, как только обнаруживает, что <tex>\mathcal{P_{N}}</tex> опустошил свой магазин. Таким образом допущенное слово по пустому стеку, будет допускаться и по заключительному состоянию, используя <tex>\varepsilon</tex> переходы в новое состояние. | '''2.''' Добавим новое допускающее состояние <tex>p</tex>, в которое автомат переходит, как только обнаруживает, что <tex>\mathcal{P_{N}}</tex> опустошил свой магазин. Таким образом допущенное слово по пустому стеку, будет допускаться и по заключительному состоянию, используя <tex>\varepsilon</tex> переходы в новое состояние. | ||
| − | '''3.''' Каждый переход <tex>\mathcal{P_{N}}</tex> есть и у автомата <tex>\mathcal{P}_{T}</tex>. Тогда, согласно введенным начальному и заключительному состоянию, автомат <tex>\mathcal{P}_{T}</tex> может совершить следующие действия: <tex>(s, w, Z_{1})\vdash (s_{0}, w, Z_{0} Z_{1})\vdash^{*} (q, \varepsilon, Z_{1})\vdash (p, \varepsilon,Z_{1}) </tex>, что означает <tex>\mathcal{P}_{T}</tex> допускает слово <tex>w</tex> по заключительному состоянию <tex>p</tex>. | + | '''3.''' Каждый переход <tex>\mathcal{P_{N}}</tex> есть и у автомата <tex>\mathcal{P}_{T}</tex>. Тогда, согласно введенным начальному и заключительному состоянию, автомат <tex>\mathcal{P}_{T}</tex> может совершить следующие действия: <tex>(s, w, Z_{1})\vdash (s_{0}, w, Z_{0} Z_{1})\vdash^{*} (q, \varepsilon, Z_{1})\vdash (p, \varepsilon,Z_{1}) </tex>, что означает <tex>\mathcal{P}_{T}</tex> допускает слово <tex>w</tex> по заключительному состоянию <tex>p</tex>. }} |
</font> | </font> | ||
Версия 06:18, 29 октября 2010
Допуск по заключительному состоянию
| Определение: |
| Пусть - МП-автомат. Тогда языком, допускаемым автоматом по заключительному состоянию, является для некоторого состояния и произвольной магазинной цепочки . Начиная с стартовой вершины и с на входе, автомат прочитывает слово и достигает допускающего состояния. Содержимое магазина в этот момент не имеет значения. |
Допуск по пустому магазину
| Определение: |
| Для МП-автомата определим множество допускающих слов как , где - произвольное состояние. Таким образом автомат прочитывает слово , полностью опустошив свой магазин. Множество заключительных состояний не имеет значение. |
Эквивалентность автоматов
| Теорема: |
Классы языков, допускаемых МП-автоматами по заключительному состоянию и по пустому магазину (стеку), совпадают. |
| Доказательство: |
|
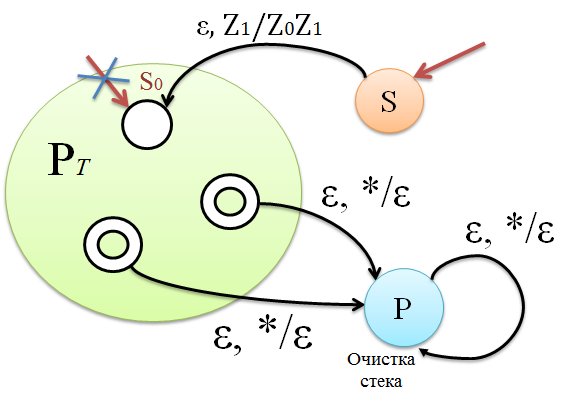
Исходя из МП-автомата , допускающего язык по заключительному состоянию, построим другой МП-автомат , который допускает язык по пустому стеку. 1. Добавим переходы по из каждого допускающего состояния автомата в новое состояние , которое отвечает за очистку стека. Находясь в состоянии , автомат опустошает свой магазин и ничего не прочитывает на входе. Таким образом, как только исходный автомат приходит в допускающее состояние, прочитав слово , опустошает свой магазин, также прочитав слово . 2. Во избежание случая, когда может опустошить свой магазин без допуска, использует свой маркер дна . Добавление нового стартового состояния позволяет затолкнуть маркер автомата в магазин и перейти в стартовое состояние . 3. Каждый переход есть и у автомата , символ хранится в магазине под всеми символами из и является символом, по которому нет переходов в . Тогда может совершить следующие действия: , что означает допускает слово по пустому магазину.
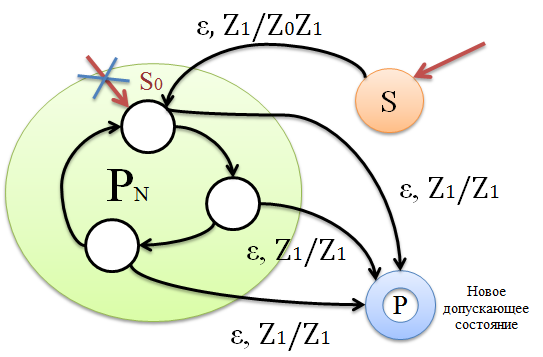
Исходя из МП-автомата , допускающего язык по пустому стеку, построим МП-автомат , допускающий по заключительному состоянию. 1. Добавим новый символ , не принадлежащий , который будем маркером дна магазина нового автомата, позволяющий узнать, когда опустошает свой магазин. Если построенный автомат видит на вершине стека свой маркер, то он знает, что опустошает свой магазин на этом же входе. 2. Добавим новое допускающее состояние , в которое автомат переходит, как только обнаруживает, что опустошил свой магазин. Таким образом допущенное слово по пустому стеку, будет допускаться и по заключительному состоянию, используя переходы в новое состояние. 3. Каждый переход есть и у автомата . Тогда, согласно введенным начальному и заключительному состоянию, автомат может совершить следующие действия: , что означает допускает слово по заключительному состоянию . |