Участница:Mariashka — различия между версиями
Mariashka (обсуждение | вклад) |
Mariashka (обсуждение | вклад) |
||
| Строка 17: | Строка 17: | ||
=== Нахождение правых повтров === | === Нахождение правых повтров === | ||
| − | Рассмотрим строку <tex>t = | + | Рассмотрим строку <tex>t = u + v</tex>, пусть <tex>shift</tex> {{---}} индекс начала <tex>t</tex> в исходной строке <tex>s</tex> |
# Предподсчитаем следующие массивы c помощью z-функции: | # Предподсчитаем следующие массивы c помощью z-функции: | ||
| Строка 45: | Строка 45: | ||
=== Нахождение левых повтров === | === Нахождение левых повтров === | ||
| − | Рассмотрим строку <tex>t = | + | Рассмотрим строку <tex>t = u + v</tex>, пусть <tex>shift</tex> {{---}} индекс начала <tex>t</tex> в исходной строке <tex>s</tex> |
# Предподсчитаем следующие массивы с помощью z-функции: | # Предподсчитаем следующие массивы с помощью z-функции: | ||
Версия 07:11, 29 апреля 2015
| Определение: |
| Повтором (англ. repeatition) называется непустая строка вида |
Алгоритм Мейна-Лоренца (англ. Main-Lorentz algorithm) — алгоритм на строках, позволяющий найти все повторы в строке за
Содержание
Алгоритм
Так как повторов строке , мы не можем хранить их в явном виде. Будем хранить повторы блоками вида , где — это длина повтора, а — промежуток индексов, в которых заканчиваются повторы такой длины. Для каждой длины может быть несколько блоков.
Данный алгоритм — это алгоритм типа "разделяй и властвуй":
- Разделим строку пополам
- Заметим, что повторы делятся на две группы: пересекающие и не пересекающие границу раздела
- Рекурсивно запустимся от каждой половинки — так мы найдем повторы, которые не пересекают границу раздела
- Далее рассмотрим процесс нахождения повторов, которые пересекают границу раздела
Повторы, пересекающие границу раздела, можно разделить на две группы по положению центра повтора: правые и левые.
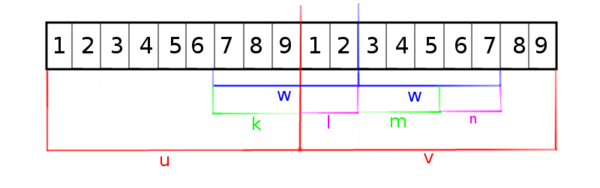
Нахождение правых повтров
Рассмотрим строку , пусть — индекс начала в исходной строке
- Предподсчитаем следующие массивы c помощью z-функции:
- , то есть наибольший общий префикс строк v[i..v.len] и v
- , то есть наибольший общий суффикс строк v[1..i] и u
- Переберем длину повтора и будем искать все повторы такой длины. Для этого для каждого получим интервал индексов конца повтора в строке : (позднее покажем, как это сделать).
- Добавим к ответу, учитывая смещение в исходной строке :
Итоговая асимптотика:
Докажем следующее утверждение для нахождения интервала :
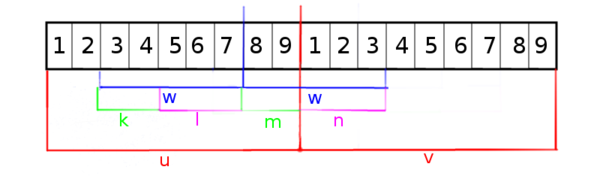
Нахождение левых повтров
Рассмотрим строку , пусть — индекс начала в исходной строке
- Предподсчитаем следующие массивы с помощью z-функции:
- , то есть наибольший общий префикс строк u[i..u.len] и v
- , где — наибольший общий суффикс
- Переберем длину повтора и будем искать все повторы такой длины. Для этого для каждого получим интервал индексов конца повтора в строке : (позднее покажем, как это сделать).
- Добавим к ответу, учитывая смещение в исходной строке :
Итоговая асимптотика:
Докажем следующее утверждение для нахождения интервала :
Асимптотика
Ассимптотика алгоритма "разделяй и властвуй", каждый рекурсивный запуск которого линеен относительно длины строки, из рекурентного соотношения (аналогичное доказательство для сортировки слиянием).
Количество блоков в ответе также будет , так как при каждом рекрсивном запуске добавляется блоков для каждой рассмотренной длины повтора, а их количество линейно относительно длины строки.
Источники
- Main, M., Lorentz, R.J. — An O(n log n) Algorithm for Finding All Repetitions in a String. 1982
- Билл Смит — Методы и алгоритмы вычислений на строках. Пер. с англ.— М.:Издательский дом "Вильямс", 2006. ISBN 5-8459-1081-1