Обсуждение участницы:Анна — различия между версиями
Анна (обсуждение | вклад) (→Алгоритм разделения АВЛ-дерева на два, где в первом дереве все ключи меньше заданного x, а во втором - больше) |
Анна (обсуждение | вклад) |
||
| Строка 13: | Строка 13: | ||
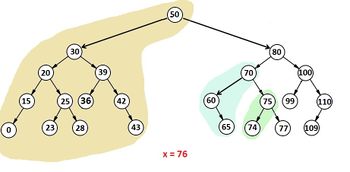
Рассмотри пример (рис. 1). Цветом выделены поддеревья, которые после разделения должны отойти в дерево <tex>T_{1}</tex>. <tex>x = 76</tex>. | Рассмотри пример (рис. 1). Цветом выделены поддеревья, которые после разделения должны отойти в дерево <tex>T_{1}</tex>. <tex>x = 76</tex>. | ||
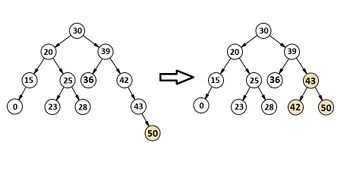
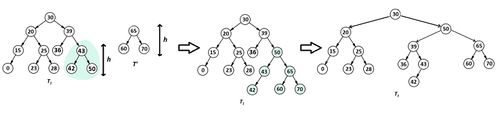
| − | Корень дерева <tex>\leqslant x</tex>, поэтому он со всем выделенным поддеревом должен отойти в дерево <tex>T_{1}</tex>. По описанному выше алгоритму отделяем это поддерево с корнем и делаем из них сбалансированное АВЛ-дерево <tex>tmpT</tex> (рис. 2). Так как это первая ситуация, в которой корень рассматриваемого поддерева был <tex>\leqslant x</tex>, <tex>tmpT</tex> становится <tex>T_{1}</tex>. Далее по сохраненной ссылке спускаемся в правое поддерево. Его корень <tex>> x</tex>. Следовательно, строим из него и его правого поддерева <tex>T_{2}</tex> и спускаемся в левое поддерево. Снова корень <tex>\leqslant x</tex>. | + | Корень дерева <tex>\leqslant x</tex>, поэтому он со всем выделенным поддеревом должен отойти в дерево <tex>T_{1}</tex>. По описанному выше алгоритму отделяем это поддерево с корнем и делаем из них сбалансированное АВЛ-дерево <tex>tmpT</tex> (рис. 2). Так как это первая ситуация, в которой корень рассматриваемого поддерева был <tex>\leqslant x</tex>, <tex>tmpT</tex> становится <tex>T_{1}</tex>. Далее по сохраненной ссылке спускаемся в правое поддерево. Его корень <tex>> x</tex>. Следовательно, строим из него и его правого поддерева <tex>T_{2}</tex> и спускаемся в левое поддерево. Снова корень <tex>\leqslant x</tex>. Строим новое <tex>tmpT</tex> и объединяем его с уже существующим <tex>T_{1}</tex> (рис. 3). |
| + | [[Файл:AVL3.jpg|500px|thumb|left|Рис. 3. Объединение tmpT и T1.]] | ||
Версия 19:20, 19 мая 2015
Алгоритм разделения АВЛ-дерева на два, где в первом дереве все ключи меньше заданного x, а во втором - больше
Пусть у нас есть дерево . Мы должны разбить его на два дерева и такие, что и .
Предположим, что корень нашего дерева , в таком случае все левое поддерево вместе с корнем после разделения отойдет в дерево . Тогда рекурсивно спускаемся в правое поддерево и там проверяем это условие (так как часть правого поддерева тоже может содержать ключи ). Если же корень оказался , то мы спускаемся той же рекурсией, но только в левое поддерево и ищем там.
Пусть мы пришли в поддерево , корень которого . В таком случае этот корень со своим левым поддеревом должен отойти в дерево . Поэтому мы делаем следующее: запоминаем ссылку на правое поддерево , удаляем корень, запоминая его значение (не меняя конфигурацию дерева, то есть просто делаем ссылки на него NULL'ами). Таким образом, мы отделяем сбалансированное АВЛ-дерево (бывшее левое поддерево ). Делаем новую вершину со значением бывшего корня правым листом самой правой вершины и запускаем балансировку. Обозначим полученное дерево за . Теперь нам нужно объединить его с уже построенным ранее (оно может быть пустым, если мы первый раз нашли такое дерево ). Для этого мы ищем в дереве самое правое поддерево высоты, равной высоте (спускаясь от корня всегда в правые поддеревья). Делаем новое дерево , сливая и (очевидно, все ключи в меньше ключей в , поэтому мы можем это сделать). Теперь в дереве у отца вершины, в которой мы остановились при поиске дерева , правым поддеревом делаем дерево и запускаем балансировку. После нужно спуститься в правое поддерево бывшего дерева (по ссылке, которую мы ранее запомнили) и обработать его.
Если мы пришли в поддерево , корень которого , совершаем аналогичные действия: делаем NULL'ами ссылки на корень , запоминая ссылку на его левое поддерево. Делаем новую вершину со значением бывшего корня левым листом самой левой вершины и запускаем балансировку. Объединяем полученное АВЛ-дерево с уже построенным ранее аналогичным первому случаю способом, только теперь мы ищем самое левое поддерево .
Рассмотри пример (рис. 1). Цветом выделены поддеревья, которые после разделения должны отойти в дерево . .
Корень дерева , поэтому он со всем выделенным поддеревом должен отойти в дерево . По описанному выше алгоритму отделяем это поддерево с корнем и делаем из них сбалансированное АВЛ-дерево (рис. 2). Так как это первая ситуация, в которой корень рассматриваемого поддерева был , становится . Далее по сохраненной ссылке спускаемся в правое поддерево. Его корень . Следовательно, строим из него и его правого поддерева и спускаемся в левое поддерево. Снова корень . Строим новое и объединяем его с уже существующим (рис. 3).