АВЛ-дерево с O(1) бит в каждом узле — различия между версиями
Kyper (обсуждение | вклад) (Новая страница: «'''В данной модификации нам заранее будет известно количество памяти, которое мы должны в...») |
Kyper (обсуждение | вклад) м (→Идея) |
||
| Строка 2: | Строка 2: | ||
== Идея == | == Идея == | ||
| − | В обычной реализации АВЛ-дерева в каждом узле мы хранили высоту этого узла. Теперь же мы будем хранить только "перекос" дерева, так как высоты левых и правых поддеревьев в АВЛ-дереве отличаются максимум на 1. Таким образом в каждом узле будет хранится | + | В обычной реализации АВЛ-дерева в каждом узле мы хранили высоту этого узла. Теперь же мы будем хранить только "перекос" дерева, так как высоты левых и правых поддеревьев в АВЛ-дереве отличаются максимум на <math>1</math>. Таким образом в каждом узле будет хранится <math>+1</math> - если высота левого поддерева больше высоты правого, <math>0</math> - если высота левого равна высоте правого, и <math>-1</math> - если высота левого поддерева меньше высоты правого. |
== Операции == | == Операции == | ||
Версия 20:37, 3 июня 2015
В данной модификации нам заранее будет известно количество памяти, которое мы должны выделить на узел дерева.
Идея
В обычной реализации АВЛ-дерева в каждом узле мы хранили высоту этого узла. Теперь же мы будем хранить только "перекос" дерева, так как высоты левых и правых поддеревьев в АВЛ-дереве отличаются максимум на . Таким образом в каждом узле будет хранится - если высота левого поддерева больше высоты правого, - если высота левого равна высоте правого, и - если высота левого поддерева меньше высоты правого.
Операции
Все операции делаются так же, как и в обычной реализации АВЛ-дерева[1], то есть мы добавили/удалили вершину, идем вверх и пересчитываем "перекосы" вершин. Нам интересна операция балансировки.
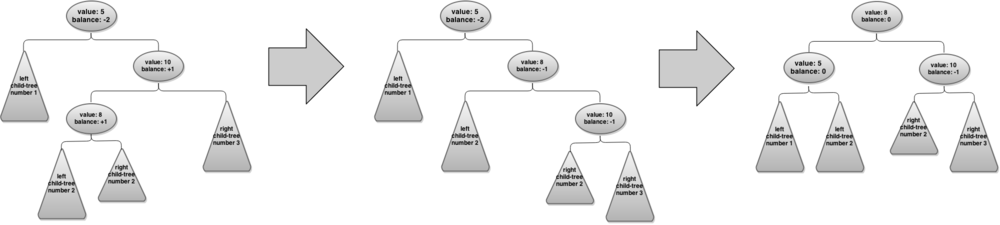
Балансировка
Для исправления "перекосов" вершин в подобной ситуации, достаточно знать "перекосы" двух(для большого вращения - трех) вершин перед поворотом, и исправить значения этих же вершин после поворота.