Поиск k-ой порядковой статистики за линейное время — различия между версиями
(→Анализ времени работы алгоритма) |
|||
| Строка 35: | Строка 35: | ||
Пусть <tex>T(n)</tex> — время работы алгоритма для <tex>n</tex> элементов, тогда оно не больше, чем сумма: | Пусть <tex>T(n)</tex> — время работы алгоритма для <tex>n</tex> элементов, тогда оно не больше, чем сумма: | ||
# времени работы на сортировку групп и разбиение по рассекающему элементу, то есть <tex>Cn</tex>; | # времени работы на сортировку групп и разбиение по рассекающему элементу, то есть <tex>Cn</tex>; | ||
| − | # времени работы для поиска медианы медиан, то есть <tex>T</tex><tex>(\dfrac{n}{5})</tex>; | + | # времени работы для поиска медианы медиан, то есть <tex>T</tex><tex>\left(\dfrac{n}{5}\right)</tex>; |
# времени работы для поиска <tex>k</tex>-го элемента в одной из двух частей массива, то есть <tex>T(s)</tex>, где <tex>s</tex> — количество элементов в этой части. Но <tex>s</tex> не превосходит <tex>\dfrac{7n}{10}</tex>, так как чисел, меньших рассекающего элемента, не менее <tex>\dfrac{3n}{10}</tex> — это <tex>\dfrac{n}{10}</tex> медиан, меньших медианы медиан, плюс не менее <tex>\dfrac{2n}{10}</tex> элементов, меньших этих медиан. С другой стороны, чисел, больших рассекающего элемента, так же не менее <tex>\dfrac{3n}{10}</tex>, следовательно <tex> s \leqslant </tex> <tex>\dfrac{7n}{10}</tex>, то есть в худшем случае <tex> s = </tex> <tex>\dfrac{7n}{10}</tex>. | # времени работы для поиска <tex>k</tex>-го элемента в одной из двух частей массива, то есть <tex>T(s)</tex>, где <tex>s</tex> — количество элементов в этой части. Но <tex>s</tex> не превосходит <tex>\dfrac{7n}{10}</tex>, так как чисел, меньших рассекающего элемента, не менее <tex>\dfrac{3n}{10}</tex> — это <tex>\dfrac{n}{10}</tex> медиан, меньших медианы медиан, плюс не менее <tex>\dfrac{2n}{10}</tex> элементов, меньших этих медиан. С другой стороны, чисел, больших рассекающего элемента, так же не менее <tex>\dfrac{3n}{10}</tex>, следовательно <tex> s \leqslant </tex> <tex>\dfrac{7n}{10}</tex>, то есть в худшем случае <tex> s = </tex> <tex>\dfrac{7n}{10}</tex>. | ||
Тогда получаем, что | Тогда получаем, что | ||
| − | <tex>T(n) \leqslant T</tex><tex>(\dfrac{n}{5})</tex><tex> + T</tex><tex>(\dfrac{7n}{10})</tex><tex> + Cn </tex> | + | <tex>T(n) \leqslant T</tex><tex>\left(\dfrac{n}{5}\right)</tex><tex> + T</tex><tex>\left(\dfrac{7n}{10}\right)</tex><tex> + Cn </tex> |
Покажем, что для всех <tex> n </tex> выполняется неравенство <tex>T(n) \leqslant 10Cn </tex>. | Покажем, что для всех <tex> n </tex> выполняется неравенство <tex>T(n) \leqslant 10Cn </tex>. | ||
| Строка 45: | Строка 45: | ||
Докажем по индукции: | Докажем по индукции: | ||
# Предположим, что наше неравенство <tex>T(n) \leqslant 10Cn </tex> выполняется при малых <tex> n </tex>, для некоторой достаточно большой константы <tex> C </tex>. | # Предположим, что наше неравенство <tex>T(n) \leqslant 10Cn </tex> выполняется при малых <tex> n </tex>, для некоторой достаточно большой константы <tex> C </tex>. | ||
| − | # Тогда, по предположению индукции, <tex>T</tex><tex>(\dfrac{n}{5})</tex><tex> \leqslant 10C </tex><tex>\dfrac{n}{5}</tex><tex> = 2Cn</tex> и <tex> T</tex><tex>(\dfrac{7n}{10})</tex><tex> \leqslant 10C </tex><tex>\dfrac{7n}{10}</tex><tex> = 7Cn</tex>, тогда | + | # Тогда, по предположению индукции, <tex>T</tex><tex>\left(\dfrac{n}{5}\right)</tex> <tex> \leqslant 10C </tex><tex>\dfrac{n}{5}</tex> <tex> = 2Cn</tex> и <tex> T</tex><tex>\left(\dfrac{7n}{10}\right)</tex> <tex> \leqslant 10C </tex><tex>\dfrac{7n}{10}</tex> <tex> = 7Cn</tex>, тогда |
| − | <tex>T(n) \leqslant T</tex><tex>(\dfrac{n}{5})</tex><tex> + T</tex><tex>(\dfrac{7n}{10})</tex><tex> + Cn = 2Cn + 7Cn + Cn = 10Cn \Rightarrow T(n) \leqslant 10Cn</tex> | + | <tex>T(n) \leqslant T</tex><tex>\left(\dfrac{n}{5}\right)</tex> <tex> + T</tex><tex>\left(\dfrac{7n}{10}\right)</tex> <tex> + Cn = 2Cn + 7Cn + Cn = 10Cn \Rightarrow T(n) \leqslant 10Cn</tex> |
Так как <tex>T(n) \leqslant 10Cn </tex>, то время работы алгоритма <tex>O(n)</tex> | Так как <tex>T(n) \leqslant 10Cn </tex>, то время работы алгоритма <tex>O(n)</tex> | ||
Версия 16:43, 4 июня 2015
Алгоритм был разработан Р. Ривестом (R. Rivest) и Р. Тарьяном (R. Tarjan).
Содержание
Идея алгоритма
Этот алгоритм является модификацией алгоритма поиска k-ой порядковой статистики. Важное отличие заключается в том, что время работы алгоритма в наихудшем случае — , где — количество элементов в множестве. Главная идея алгоритма заключается в том, чтобы гарантировать хорошее разбиение массива. Алгоритм выбирает такой рассекающий элемент, что количество чисел, которые меньше рассекающего элемента, не менее . Элементов же больших опорного элемента, также не менее . Благодаря этому алгоритм работает за линейное время в любом случае.
Описание алгоритма
- Все элементов входного массива разбиваются на группы по пять элементов, в последней группе будет элементов. Эта группа может оказаться пустой при кратным .
- Сначала сортируется каждая группа, затем из каждой группы выбирается медиана.
- Путем рекурсивного вызова шага определяется медиана из множества медиан (верхняя медиана в случае чётного количества), найденных на втором шаге. Найденный элемент массива используется как рассекающий (за обозначим его индекс).
- Массив делится относительно рассекающего элемента .
- Если , то возвращается значение . Иначе запускается рекурсивно поиск элемента в одной из частей массива: -ой статистики в левой части при или -ой статистики в правой части при
Пример работы алгоритма
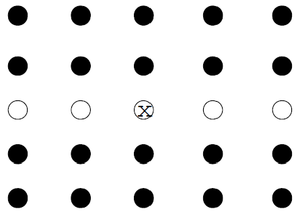
Рассмотрим работу алгоритма на массиве из элементов, обозначенных кружками.
На вход подается массив, разобьем элементы на группы по 5 элементов. Отсортируем элементы каждой группы и выберем медианы. Полученные медианы групп отмечены белыми кружками.
Рекурсивно вызовемся от медиан групп и получим рассекающий элемент. На рисунке он обозначен белым кружком, внутри которого изображен символ .
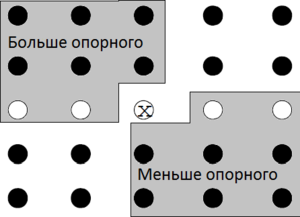
На рисунке обозначены закрашенные области, в левом верхнем и в правом нижнем углах. В эти области попали все элементы, которые точно меньше или больше рассекающего элемента, соответственно. В каждой области по элементов, всего же в массиве , то есть мы получили хорошее (то есть соответствующее нашему утверждению) разбиение массива относительно опорного элемента, так как . Теперь докажем, что алгоритм также хорошо выбирает опорный элемент и в общем случае.
Cначала определим нижнюю границу для количества элементов, превышающих по величине рассекающий элемент . В общем случае как минимум половина медиан, найденных на втором шаге, больше или равны медианы медиан . Таким образом, как минимум групп содержат по превышающих величину , за исключение группы, в которой меньше элементов и ещё одной группы, содержащей сам элемент . Таким образом получаем, что количество элементов больших , не менее .
Проведя аналогичные рассуждения для элементов, которые меньше по величине, чем рассекающий элемент , мы получим, что как минимум меньше, чем элемент . Теперь проведем анализ времени работы алгоритма.
Анализ времени работы алгоритма
Пусть — время работы алгоритма для элементов, тогда оно не больше, чем сумма:
- времени работы на сортировку групп и разбиение по рассекающему элементу, то есть ;
- времени работы для поиска медианы медиан, то есть ;
- времени работы для поиска -го элемента в одной из двух частей массива, то есть , где — количество элементов в этой части. Но не превосходит , так как чисел, меньших рассекающего элемента, не менее — это медиан, меньших медианы медиан, плюс не менее элементов, меньших этих медиан. С другой стороны, чисел, больших рассекающего элемента, так же не менее , следовательно , то есть в худшем случае .
Тогда получаем, что
Покажем, что для всех выполняется неравенство .
Докажем по индукции:
- Предположим, что наше неравенство выполняется при малых , для некоторой достаточно большой константы .
- Тогда, по предположению индукции, и , тогда
Так как , то время работы алгоритма
Источники инфомации
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ — Вильямс, 2013. — 1328 с. — ISBN 978-5-8459-1794-2
- Wikipedia — Selection algorithm