АВЛ-дерево с O(1) бит в каждом узле — различия между версиями
Kyper (обсуждение | вклад) |
Kyper (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
=== Идея === | === Идея === | ||
В обычной реализации АВЛ-дерева[http://neerc.ifmo.ru/wiki/index.php?title=%D0%90%D0%92%D0%9B-%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D0%BE] в каждом узле мы хранили высоту этого узла. Так как высоты левых и правых поддеревьев в АВЛ-дереве отличаются на <tex>1</tex> (при разбалансировке вершины разность поддеревьев будет максимум <tex>2</tex> или <tex>-2</tex>), то мы будем хранить не всю высоту дерева, а некоторое число, которое будет показывать разницу между высотами его правой и левой ветки - назовём его ''фактор баланса''. Таким образом в каждом узле будет хранится <tex>1</tex> - если высота правого поддерева выше левого, <tex>0</tex> - если высоты равны, и <tex>-1</tex> - если правое поддерево выше левого. | В обычной реализации АВЛ-дерева[http://neerc.ifmo.ru/wiki/index.php?title=%D0%90%D0%92%D0%9B-%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D0%BE] в каждом узле мы хранили высоту этого узла. Так как высоты левых и правых поддеревьев в АВЛ-дереве отличаются на <tex>1</tex> (при разбалансировке вершины разность поддеревьев будет максимум <tex>2</tex> или <tex>-2</tex>), то мы будем хранить не всю высоту дерева, а некоторое число, которое будет показывать разницу между высотами его правой и левой ветки - назовём его ''фактор баланса''. Таким образом в каждом узле будет хранится <tex>1</tex> - если высота правого поддерева выше левого, <tex>0</tex> - если высоты равны, и <tex>-1</tex> - если правое поддерево выше левого. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Операции === | === Операции === | ||
| − | '''Операция добавления''' | + | '''Операция добавления''' <br> |
Пусть нам надо добавить ключ <tex>t</tex>. Будем спускаться по дереву, как при поиске ключа <tex>t</tex>. Если мы стоим в вершине <tex>a</tex> и нам надо идти в поддерево, которого нет, то делаем ключ <tex>t</tex> листом, а вершину <tex>a</tex> его корнем. Пересчитываем баланс данного узла <tex>a</tex>. Дальше начинаем подниматься верх по дереву, исправляя балансы попутных узлов. Если мы поднялись в вершину <tex>i</tex> из левого поддерева, то баланс уменьшается на единицу, если из правого, то увеличивается на единицу. Если мы пришли в вершину и её баланс стал равным <tex>1</tex> или <tex>-1</tex>, то это значит, что высота поддерева изменилась и подъём продолжается. Если пришли в вершину и её баланс стал равным <tex>2</tex> или <tex>-2</tex>, то делаем балансировку. Если в результате изменения узла, фактор баланса стал равен нулю, то останавливаемся, иначе продолжаем подъём. | Пусть нам надо добавить ключ <tex>t</tex>. Будем спускаться по дереву, как при поиске ключа <tex>t</tex>. Если мы стоим в вершине <tex>a</tex> и нам надо идти в поддерево, которого нет, то делаем ключ <tex>t</tex> листом, а вершину <tex>a</tex> его корнем. Пересчитываем баланс данного узла <tex>a</tex>. Дальше начинаем подниматься верх по дереву, исправляя балансы попутных узлов. Если мы поднялись в вершину <tex>i</tex> из левого поддерева, то баланс уменьшается на единицу, если из правого, то увеличивается на единицу. Если мы пришли в вершину и её баланс стал равным <tex>1</tex> или <tex>-1</tex>, то это значит, что высота поддерева изменилась и подъём продолжается. Если пришли в вершину и её баланс стал равным <tex>2</tex> или <tex>-2</tex>, то делаем балансировку. Если в результате изменения узла, фактор баланса стал равен нулю, то останавливаемся, иначе продолжаем подъём. | ||
| − | '''Операция удаления''' | + | |
| + | '''Операция удаления''' <br> | ||
Если вершина - лист, то просто удалим её, иначе найдём ближайшую по значению вершину <tex>a</tex>, поменяем ее местами с удаляемой вершиной и удалим. От удалённой вершины будем подниматься вверх к корню и пересчитывать фактор баланса вершин. Если мы поднялись в вершину <tex>i</tex> из левого поддерева, то фактор баланса увеличивается на единицу, если из правого, то уменьшается на единицу. Если мы пришли в вершину и её баланс стал равным <tex>1</tex> или <tex>-1</tex>, то это значит, что высота поддерева не изменилась и подъём можно остановить. Если баланс вершины стал равным нулю, то высота поддерева уменьшилась и подъём нужно продолжить. Если баланс стал равным <tex>2</tex> или <tex>-2</tex>, то делаем балансировку. Если в результате изменения узла, фактор баланса стал равен нулю, то подъём продолжается, иначе останавливается. | Если вершина - лист, то просто удалим её, иначе найдём ближайшую по значению вершину <tex>a</tex>, поменяем ее местами с удаляемой вершиной и удалим. От удалённой вершины будем подниматься вверх к корню и пересчитывать фактор баланса вершин. Если мы поднялись в вершину <tex>i</tex> из левого поддерева, то фактор баланса увеличивается на единицу, если из правого, то уменьшается на единицу. Если мы пришли в вершину и её баланс стал равным <tex>1</tex> или <tex>-1</tex>, то это значит, что высота поддерева не изменилась и подъём можно остановить. Если баланс вершины стал равным нулю, то высота поддерева уменьшилась и подъём нужно продолжить. Если баланс стал равным <tex>2</tex> или <tex>-2</tex>, то делаем балансировку. Если в результате изменения узла, фактор баланса стал равен нулю, то подъём продолжается, иначе останавливается. | ||
| + | |||
| + | === Балансировка === | ||
| + | Опишем операции балансировки, а именно малый поворот, большой поворот и случаи их возникновения. Балансировка нам нужна для операций добавления и удаления узла. Для исправления факторов баланса, достаточно знать факторы баланса двух(в случае большого поворота-трех) вершин перед поворотом, и исправить значения этих же вершин после поворота. Обозначим фактор баланса вершины <tex>i</tex> как <tex>balance[i]</tex>. | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | !Тип вращения | ||
| + | !Иллюстрация | ||
| + | !Факторы балансов до вращения | ||
| + | !Факторы балансов после вращения | ||
| + | |- | ||
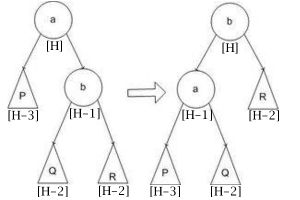
| + | |'''Малое вращение''' | ||
| + | | [[Файл:avl_u1.jpg|2000x200px]] | ||
| + | | | ||
| + | '''1 вариант:''' <tex>balance[a] = -2</tex> и <tex>balance[b] = -1</tex> | ||
| + | |||
| + | |||
| + | '''2 вариант:''' <tex>balance[a] = -2</tex> и <tex>balance[b] = 0</tex>. | ||
| + | | | ||
| + | |||
| + | '''1 вариант:''' <tex>balance[a] = 0</tex> и <tex>balance[b] = 0</tex> | ||
| + | |||
| + | |||
| + | '''2 вариант:''' <tex>balance[a] = -1</tex> и <tex>balance[b] = 1</tex> | ||
| + | |||
| + | |- | ||
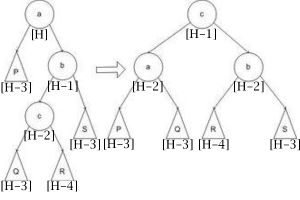
| + | |'''Большое вращение''' | ||
| + | | [[Файл:avl_u2.jpg|2000x200px]] | ||
| + | | | ||
| + | '''1 вариант:''' <tex>balance[a] = -2</tex> , <tex>balance[b] = 1</tex> и <tex>balance[c] = 1</tex> | ||
| + | |||
| + | |||
| + | '''2 вариант:''' <tex>balance[a] = -2</tex>, <tex>balance[b] = 1</tex> и <tex>balance[c] = -1</tex> | ||
| + | |||
| + | |||
| + | '''3 вариант:''' <tex>balance[a] = -2</tex>, <tex>balance[b] = 1</tex> и <tex>balance[c] = 0</tex>. | ||
| + | | | ||
| + | |||
| + | '''1 вариант:''' <tex>balance[a] = 0</tex>, <tex>balance[b] = -1</tex> и <tex>balance[c] = 0</tex> | ||
| + | |||
| + | |||
| + | '''2 вариант:''' <tex>balance[a] = 1</tex>, <tex>balance[b] = 0</tex> и <tex>balance[c] = 0</tex> | ||
| + | |||
| + | |||
| + | '''3 вариант:''' <tex>balance[a] = 0</tex>, <tex>balance[b] = 0</tex> и <tex>balance[c] = 0</tex> | ||
| + | |} | ||
| + | |||
| + | |||
| + | === Примеры === | ||
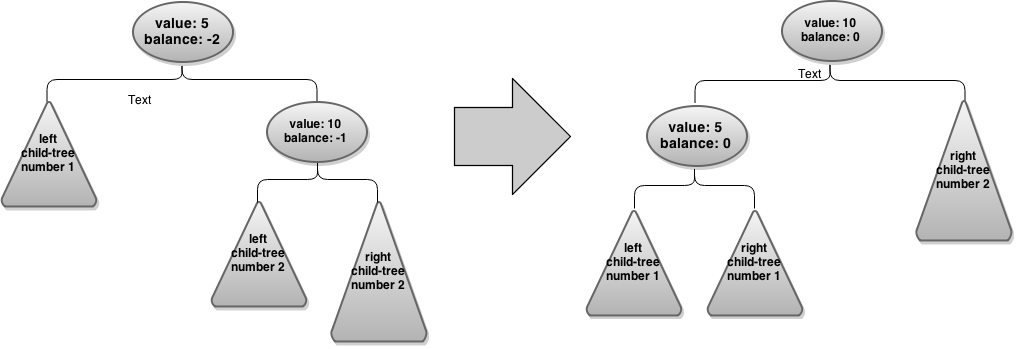
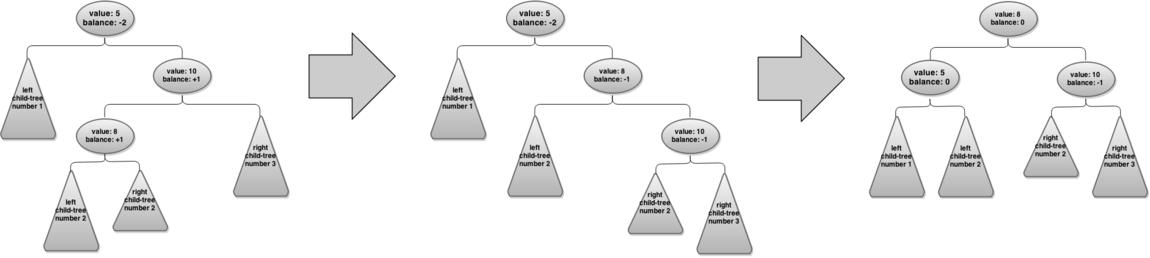
| + | Ниже приведены примеры большого и малого вращения с подписанными изменениями балансов каждой вершины, участвующей в повороте. | ||
| + | [[Файл:Avl-smallrotation.png|1150px|thumb|left|'''Первый случай: малое вращение''']] | ||
| + | [[Файл:Avl-bigrotation.png|1150px|thumb|left|'''Второй случай: большое вращение''']] | ||
| + | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
Версия 09:52, 5 июня 2015
Содержание
АВЛ-дерево с бит в каждом узле
Идея
В обычной реализации АВЛ-дерева[1] в каждом узле мы хранили высоту этого узла. Так как высоты левых и правых поддеревьев в АВЛ-дереве отличаются на (при разбалансировке вершины разность поддеревьев будет максимум или ), то мы будем хранить не всю высоту дерева, а некоторое число, которое будет показывать разницу между высотами его правой и левой ветки - назовём его фактор баланса. Таким образом в каждом узле будет хранится - если высота правого поддерева выше левого, - если высоты равны, и - если правое поддерево выше левого.
Операции
Операция добавления
Пусть нам надо добавить ключ . Будем спускаться по дереву, как при поиске ключа . Если мы стоим в вершине и нам надо идти в поддерево, которого нет, то делаем ключ листом, а вершину его корнем. Пересчитываем баланс данного узла . Дальше начинаем подниматься верх по дереву, исправляя балансы попутных узлов. Если мы поднялись в вершину из левого поддерева, то баланс уменьшается на единицу, если из правого, то увеличивается на единицу. Если мы пришли в вершину и её баланс стал равным или , то это значит, что высота поддерева изменилась и подъём продолжается. Если пришли в вершину и её баланс стал равным или , то делаем балансировку. Если в результате изменения узла, фактор баланса стал равен нулю, то останавливаемся, иначе продолжаем подъём.
Операция удаления
Если вершина - лист, то просто удалим её, иначе найдём ближайшую по значению вершину , поменяем ее местами с удаляемой вершиной и удалим. От удалённой вершины будем подниматься вверх к корню и пересчитывать фактор баланса вершин. Если мы поднялись в вершину из левого поддерева, то фактор баланса увеличивается на единицу, если из правого, то уменьшается на единицу. Если мы пришли в вершину и её баланс стал равным или , то это значит, что высота поддерева не изменилась и подъём можно остановить. Если баланс вершины стал равным нулю, то высота поддерева уменьшилась и подъём нужно продолжить. Если баланс стал равным или , то делаем балансировку. Если в результате изменения узла, фактор баланса стал равен нулю, то подъём продолжается, иначе останавливается.
Балансировка
Опишем операции балансировки, а именно малый поворот, большой поворот и случаи их возникновения. Балансировка нам нужна для операций добавления и удаления узла. Для исправления факторов баланса, достаточно знать факторы баланса двух(в случае большого поворота-трех) вершин перед поворотом, и исправить значения этих же вершин после поворота. Обозначим фактор баланса вершины как .
Примеры
Ниже приведены примеры большого и малого вращения с подписанными изменениями балансов каждой вершины, участвующей в повороте.