Целочисленный двоичный поиск

Целочисленный двоичный поиск (бинарный поиск) (англ. binary search) — алгоритм поиска объекта по заданному признаку в множестве объектов, упорядоченных по тому же самому признаку, работающий за логарифмическое время.

Схема бинарного поиска

Формулировка задачи

Пусть нам дан упорядоченный массив, состоящий только из целочисленных элементов. Требуется найти позицию, на которой находится заданный элемент. Для этой задачи мы и можем использовать двоичный поиск.

Принцип работы

Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остаётся та часть множества, где находится искомый объект. Или же, в зависимости от постановки задачи, мы можем остановить процесс, когда мы получим первый или же последний индекс вхождения элемента. Последнее условие — это левосторонний/правосторонний двоичный поиск.

Правосторонний/левосторонний целочисленный двоичный поиск

Для простоты дальнейших определений будем считать, что [math]a[0] = -\infty[/math] и что [math]a[n] = +\infty[/math].

Определение:

Правосторонний бинарный поиск (англ. rightside binary search) — бинарный поиск, с помощью которого мы ищем [math] \max\limits_{i \in [0,n]} \{i \mid a[i] \leqslant x\} [/math], где [math]a[/math] — массив, а [math]x[/math] — искомый ключ

Определение:

Левосторонний бинарный поиск (англ. leftside binary search) — бинарный поиск, с помощью которого мы ищем [math] \min\limits_{i \in [0,n]}\{i \mid a[i] \geqslant x\} [/math], где [math]a[/math] — массив, а [math]x[/math] — искомый ключ

Использовав эти два вида двоичного поиска, мы можем найти отрезок позиций [math][l,r][/math] таких, что [math]\forall i \in [l,r] : a[i] = x[/math] и [math] \forall i \notin [l,r] : a[i] \neq x [/math]

Например:

Задан отсортированный массив [math][1, 2, 2, 2, 2, 3, 5, 8, 9, 11], x = 2[/math].

Правосторонний поиск двойки выдаст в результате [math]5[/math], в то время как левосторонний выдаст [math]2[/math] (нумерация с единицы).

От сюда следует, что количество подряд идущих двоек равно длине отрезка [math][2;5][/math], то есть [math]4[/math].

Если искомого элемента в массиве нет, то правосторонний поиск выдаст минимальный элемент, больший искомого, а левосторонний наоборот, максимальный элемент, меньший искомого.

Алгоритм двоичного поиска

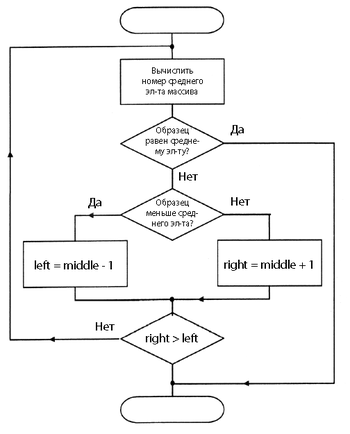
Идея поиска заключается в том, чтобы брать элемент посередине, между границами, и сравнивать его с искомым. Если искомое больше(в случае правостороннего — не меньше), чем элемент сравнения, то сужаем область поиска так, чтобы новая левая граница была равна индексу середины предыдущей области. В противном случае присваиваем это значение правой границе. Проделываем эту процедуру до тех пор, пока правая граница больше левой более чем на [math]1[/math]. В случае правостороннего бинарного поиска ответом будет индекс [math]l[/math], а в случае левостороннего — [math]r[/math].

Код

int binSearch(int[] a, int key)    // l, r - левая и правая границы
    int l = 0
    int r = len(a) + 1    
    while l < r - 1                // запускаем цикл
        m = (l + r) / 2            // m — середина области поиска
        if a[m] < key
            l = m
        else 
            r = m                  // сужение границ
    return r

В случае правостороннего поиска изменится знак сравнения при сужении границ на [math]a[m] \leqslant k[/math].

Инвариант цикла: пусть левый индекс не больше искомого элемента, а правый — строго больше, тогда если [math]l = r - 1[/math], то понятно, что [math]l[/math] — самое правое вхождение (так как следующее уже больше).

Несколько слов об эвристиках

Эвристика с завершением поиска, при досрочном нахождении искомого элемента

Заметим, что если нам необходимо просто проверить наличие элемента в упорядоченном множестве, то можно использовать любой из правостороннего и левостороннего поиска. При этом будем на каждой итерации проверять "не попали ли мы в элемент, равный искомому", и в случае попадания заканчивать поиск.

Эвристика с запоминанием ответа на предыдущий запрос

Пусть дан отсортированный массив чисел, упорядоченных по неубыванию. Также пусть запросы приходят в таком порядке, что каждый следующий не меньше, чем предыдущий. Для ответа на запрос будем использовать левосторонний двоичный поиск. При этом после того как обработался первый запрос, запомним чему равно [math]l[/math], запишем его в переменную [math]startL[/math]. Когда будем обрабатывать следующий запрос, то проинициализируем левую границу как [math]startL[/math]. Заметим, что все элементы, которые лежат не правее [math]startL[/math], строго меньше текущего искомого элемента, так как они меньше предыдущего запроса, а значит и меньше текущего. Значит инвариант цикла выполнен.

Применение двоичного поиска на неотсортированных массивах

Применение поиска на циклически сдвинутом отсортированном массиве

Пусть отсортированный массив, все элементы которого различны, был циклически сдвинут, тогда новый полученный массив состоит из двух отсортированных. Используем двоичный поиск, чтобы найти индекс последнего элемента первого из этих массивов. Для этого, в реализации двоичного поиска заменим условие в [math]if[/math] на [math]a[m] \gt a[n][/math], тогда в [math]r[/math] будет содержаться искомый индекс. Далее мы можем воспользоваться двоичный поиском искомого элемента [math]key[/math], просто запустив его два раза: на массиве [math][0, r][/math] и массиве [math][r + 1, n][/math].

См. также

• Вещественный двоичный поиск
• Троичный поиск
• Поиск с помощью золотого сечения
• Интерполяционный поиск

Источники информации

• Д. Кнут - Искусство программирования (Том 3, 2-е издание)
• Википедия - двоичный поиск
• Интересная статья про типичные ошибки
• Бинарный поиск на algolist