Суффиксный массив — различия между версиями
м (→Псевдокод) |
(доказательство, пример) |
||
| Строка 26: | Строка 26: | ||
=== Вариант для минимально возможного === | === Вариант для минимально возможного === | ||
Для начала вместо каждого символа строки поставим символ из бесконечного алфавита в промежуточную строку <tex>tmp</tex>, как в решении выше. Пусть, мы рассматриваем <tex>i</tex>-й в лексикографическом порядке суффикс (т.е. и <tex>i</tex>-й символ строки). Его первый символ будет равен первому символу предущего в лексикографическом порядке суффикса, если <tex>tmp[sa[i - 1] + 1] < tmp[sa[i] + 1]</tex>, т.е. и их строки без первого символа так же в лексикографическом порядке. Иначе он должен быть больше, т.к. рассматриваемый суффикс следующий в лексикографическом порядке. | Для начала вместо каждого символа строки поставим символ из бесконечного алфавита в промежуточную строку <tex>tmp</tex>, как в решении выше. Пусть, мы рассматриваем <tex>i</tex>-й в лексикографическом порядке суффикс (т.е. и <tex>i</tex>-й символ строки). Его первый символ будет равен первому символу предущего в лексикографическом порядке суффикса, если <tex>tmp[sa[i - 1] + 1] < tmp[sa[i] + 1]</tex>, т.е. и их строки без первого символа так же в лексикографическом порядке. Иначе он должен быть больше, т.к. рассматриваемый суффикс следующий в лексикографическом порядке. | ||
| + | |||
| + | ==== Пример ==== | ||
| + | Дан суффиксный массив [7, 5, 1, 3, 6, 2, 4]. | ||
| + | [[Файл:ExampleSuffixArray.png]] | ||
==== Псевдокод ==== | ==== Псевдокод ==== | ||
| Строка 40: | Строка 44: | ||
s[i] = alphabet[cur] | s[i] = alphabet[cur] | ||
'''return''' s | '''return''' s | ||
| + | |||
| + | ==== Доказательство минимальности ==== | ||
| + | Докажем от противного. Пусть, есть решение в котором использовано меньше букв. Тогда найдется позиция в которой, наше решение отличается от минимального, причем в минимальном остается та же буква, как в предыдущем суффиксе, а в нашем появляется новая. Рассмотрим эти два подряд идущих суффикса. В решении выше добавится новая буква, только если продолжение первого суффикса лексикографически больше, чем продолжение второго. Получается, что в минимальном решении первый суффикс лексикографически больше, чем второй, что неверно. Пришли к противоречию. | ||
== Применения == | == Применения == | ||
Версия 22:53, 10 июня 2015
| Определение: |
| Cуффиксным массивом (англ. suffix array) строки называется массив целых чисел от до , такой, что суффикс — -й в лексикографическом порядке среди всех непустых суффиксов строки . |
Содержание
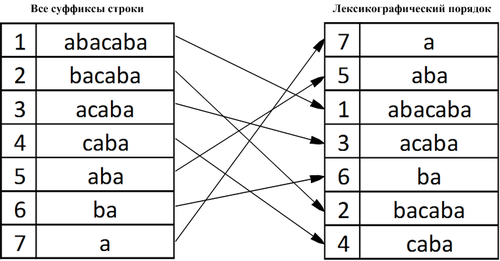
Пример
Значит, суффиксный массив для строки равен .
Восстановление строки по суффиксному массиву
| Задача: |
| Дан суффиксный массив некоторой строки , необходимо восстановить строку за время . |
Вариант для бесконечного алфавита
Так как наш алфавит не ограничен, можно -й в лексикографическом порядке суффикс сопоставить с -й буквой в алфавите.
Псевдокод
string fromSuffixArrayToString(int[] sa):
for i = 1 to n
s[sa[i]] = alphabet[i]
return s
Вариант для минимально возможного
Для начала вместо каждого символа строки поставим символ из бесконечного алфавита в промежуточную строку , как в решении выше. Пусть, мы рассматриваем -й в лексикографическом порядке суффикс (т.е. и -й символ строки). Его первый символ будет равен первому символу предущего в лексикографическом порядке суффикса, если , т.е. и их строки без первого символа так же в лексикографическом порядке. Иначе он должен быть больше, т.к. рассматриваемый суффикс следующий в лексикографическом порядке.
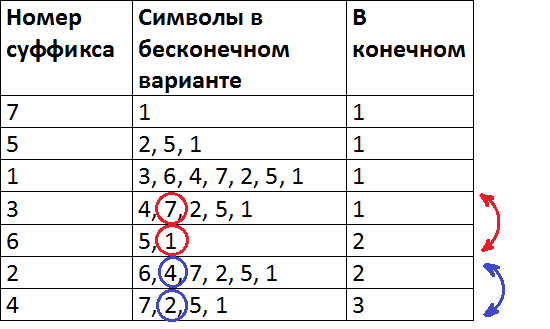
Пример
Дан суффиксный массив [7, 5, 1, 3, 6, 2, 4].
Псевдокод
string fromSuffixArrayToString(int[] sa):
for i = 1 to n
tmp[sa[i]] = alphabet[i]
cur = 1
s[1] = alphabet[1]
for i = 2 to n
j = sa[i - 1]
k = sa[i]
if tmp[j + 1] > tmp[k + 1]
cur++;
s[i] = alphabet[cur]
return s
Доказательство минимальности
Докажем от противного. Пусть, есть решение в котором использовано меньше букв. Тогда найдется позиция в которой, наше решение отличается от минимального, причем в минимальном остается та же буква, как в предыдущем суффиксе, а в нашем появляется новая. Рассмотрим эти два подряд идущих суффикса. В решении выше добавится новая буква, только если продолжение первого суффикса лексикографически больше, чем продолжение второго. Получается, что в минимальном решении первый суффикс лексикографически больше, чем второй, что неверно. Пришли к противоречию.
Применения
- Позволяет найти все вхождения образца в строку за время .
- Позволяет вычислить наибольший общий префикс (англ. longest common prefix, LCP) для всех соседних в лексикографическом порядке суффиксов строки за , то есть построить массив , где — длина наибольшего общего префикса суффиксов и .
- Позволяет найти количество различных подстрок в строке за время и дополнительной памяти.
- Позволяет найти наименьший циклический сдвиг строки за время .
- Позволяет найти максимальную по длине строку, ветвящуюся влево и вправо за время , где — время построения суффиксного массива.
См. также
- Построение суффиксного массива с помощью стандартных методов сортировки
- Алгоритм поиска подстроки в строке с помощью суффиксного массива
- Алгоритм Касаи и др.
Источники
- Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.
- MAXimal :: algo :: Суффиксный массив
- Википедия — Суффиксный массив
- Wikipedia — Suffix array
- Habrahabr — Суффиксный массив — удобная замена суффиксного дерева