Отношение связности, компоненты связности — различия между версиями
(→Сильная связность) |
|||
| Строка 7: | Строка 7: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Связность {{---}} '''отношение эквивалентности''' (equivalence relation). | + | Связность {{---}} '''[[Отношение_эквивалентности|отношение эквивалентности]]''' (equivalence relation). |
|proof= | |proof= | ||
| − | '''Рефлексивность''': <tex>\forall a \in V a \rightsquigarrow a</tex> (очевидно). | + | '''[[Рефлексивное_отношение|Рефлексивность]]''': <tex>\forall a \in V a \rightsquigarrow a</tex> (очевидно). |
| − | '''Симметричность''': <tex>a\rightsquigarrow b \Rightarrow b\rightsquigarrow a</tex> (в силу неориентированности графа). | + | '''[[Симметричное_отношение|Симметричность]]''': <tex>a\rightsquigarrow b \Rightarrow b\rightsquigarrow a</tex> (в силу неориентированности графа). |
| − | '''Транзитивность''': <tex>a\rightsquigarrow b \land b\rightsquigarrow c \Rightarrow a\rightsquigarrow c</tex>. Действительно, сначала пройдем от <tex>a</tex> до <tex>b</tex>, затем от <tex>b</tex> до <tex>c</tex>, что и означает существования пути <tex>a \rightsquigarrow c</tex>. | + | '''[[Транзитивное_отношение|Транзитивность]]''': <tex>a\rightsquigarrow b \land b\rightsquigarrow c \Rightarrow a\rightsquigarrow c</tex>. Действительно, сначала пройдем от <tex>a</tex> до <tex>b</tex>, затем от <tex>b</tex> до <tex>c</tex>, что и означает существования пути <tex>a \rightsquigarrow c</tex>. |
}} | }} | ||
| Строка 36: | Строка 36: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Слабая связность '''является отношением эквивалентности'''. | + | Слабая связность '''является [[Отношение_эквивалентности|отношением эквивалентности]]'''. |
|proof= | |proof= | ||
Аналогично доказательству соответствующей теоремы для неориентированного графа. | Аналогично доказательству соответствующей теоремы для неориентированного графа. | ||
| Строка 53: | Строка 53: | ||
{{Теорема | {{Теорема | ||
|statement= | |statement= | ||
| − | Сильная связность {{---}} '''отношение эквивалентности'''. | + | Сильная связность {{---}} '''[[Отношение_эквивалентности|отношение эквивалентности]]'''. |
|proof= | |proof= | ||
| − | '''Рефлексивность''' и '''симметричность''' очевидны. Рассмотрим '''транзитивность''': | + | '''[[Рефлексивное_отношение|Рефлексивность]]''' и '''[[Симметричное_отношение|симметричность]]''' очевидны. Рассмотрим '''[[Транзитивное_отношение|транзитивность]]''': |
<tex>(a\rightsquigarrow b \land b\rightsquigarrow a) \land (b\rightsquigarrow c \land c\rightsquigarrow b)\Leftrightarrow (a\rightsquigarrow b \land b\rightsquigarrow c) \land (c\rightsquigarrow b \land b\rightsquigarrow a) \Leftrightarrow a\rightsquigarrow c \land c\rightsquigarrow a</tex> | <tex>(a\rightsquigarrow b \land b\rightsquigarrow a) \land (b\rightsquigarrow c \land c\rightsquigarrow b)\Leftrightarrow (a\rightsquigarrow b \land b\rightsquigarrow c) \land (c\rightsquigarrow b \land b\rightsquigarrow a) \Leftrightarrow a\rightsquigarrow c \land c\rightsquigarrow a</tex> | ||
}} | }} | ||
| Строка 61: | Строка 61: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
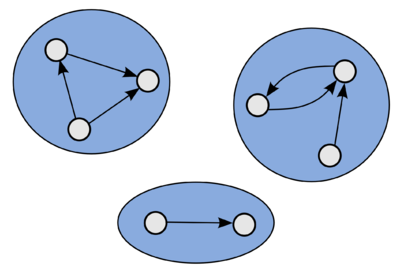
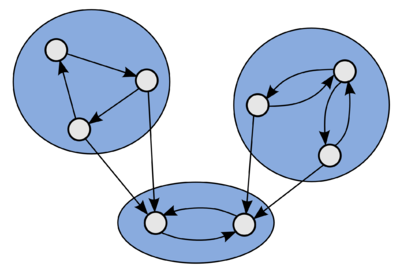
| − | Пусть <tex>G = (V, E)</tex> — ориентированный граф. '''Компонентой сильной связности''' (strongly connected component) называется класс эквивалентности множества вершин этого графа относительно сильной связности.}} | + | Пусть <tex>G = (V, E)</tex> — [[Основные_определения_теории_графов|ориентированный граф]]. '''Компонентой сильной связности''' (strongly connected component) называется класс эквивалентности множества вершин этого графа относительно сильной связности.}} |
[[Файл:Components2.png|400px|thumb|left|Пример ориентированного графа с тремя компонентами сильной связности.]] | [[Файл:Components2.png|400px|thumb|left|Пример ориентированного графа с тремя компонентами сильной связности.]] | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Ориентированный граф <tex>G = (V, E)</tex> называется '''сильно связным''' (strongly connected), если он состоит из одной компоненты сильной связности.}} | + | [[Основные_определения_теории_графов|Ориентированный граф]] <tex>G = (V, E)</tex> называется '''сильно связным''' (strongly connected), если он состоит из одной компоненты сильной связности.}} |
<br clear="all" /> | <br clear="all" /> | ||
Версия 16:49, 15 сентября 2015
Содержание
Случай неориентированного графа
| Определение: |
| Две вершины и называются связаными (adjacent), если в графе существует путь из в (обозначение: ). |
| Теорема: |
Связность — отношение эквивалентности (equivalence relation). |
| Доказательство: |
|
Рефлексивность: (очевидно). Симметричность: (в силу неориентированности графа). Транзитивность: . Действительно, сначала пройдем от до , затем от до , что и означает существования пути . |
| Определение: |
| Компонентой связности (connected component) называется класс эквивалентности относительно связности. |
| Определение: |
| Граф называется связным (connectivity graph), если он состоит из одной компоненты связности. В противном случае граф называется несвязным. |
Случай ориентированного графа
В общем случае для ориентированного графа существование пути — не симметричное отношение, поэтому вместо понятия связности различают понятие слабой и сильной связности.
Слабая связность
<wikitex>
| Определение: |
| Отношение $R(v, u)$ называется отношением слабой связности (weak connectivity), если вершины $u$ и $v$ связаны в неориентированном графе $G'$, полученном из графа $G$ удалением ориентации с рёбер. |
| Теорема: |
Слабая связность является отношением эквивалентности. |
| Доказательство: |
| Аналогично доказательству соответствующей теоремы для неориентированного графа. |
</wikitex>
Сильная связность
| Определение: |
| Отношение на вершинах графа называется отношением сильной связности (strong connectivity). |
| Теорема: |
Сильная связность — отношение эквивалентности. |
| Доказательство: |
|
Рефлексивность и симметричность очевидны. Рассмотрим транзитивность: |
| Определение: |
| Пусть — ориентированный граф. Компонентой сильной связности (strongly connected component) называется класс эквивалентности множества вершин этого графа относительно сильной связности. |
| Определение: |
| Ориентированный граф называется сильно связным (strongly connected), если он состоит из одной компоненты сильной связности. |
См. также
Источники информации
- Отношения связности для вершин неорграфа на ivtb.ru
- Харари Фрэнк Теория графов: Пер. с англ./ Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 296 с. — ISBN 978-5-397-00622-4.